Question

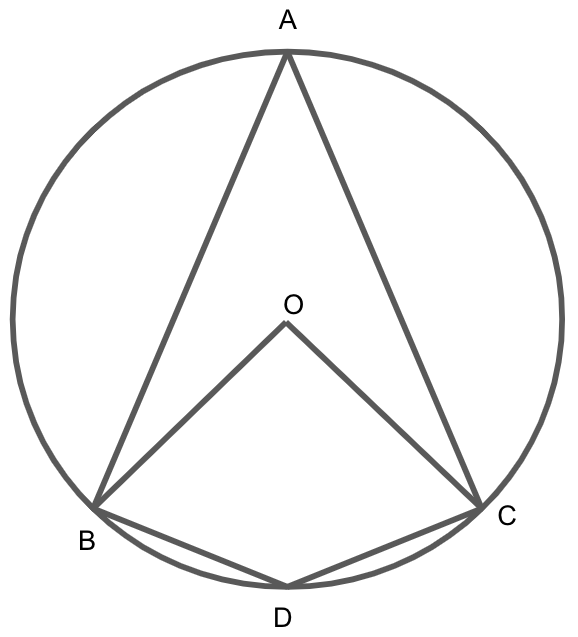
In the figure, O is the center of the circle and \[{\text{BA}} = {\text{AC}}\]. If \[\angle {\text{ABC}} = 50^\circ \], find \[\angle {\text{BOC}}\] and \[\angle {\text{BDC}}\].

Answer 1

Hint: First we will join BC in the given diagram. Then we will consider triangle \[\Delta {\text{ABC}}\] and use that \[{\text{BA}} = {\text{AC}}\] to prove it is an isosceles triangle and the two angles inclined on equal and non-equal lines are same. Then we will use the angle sum property of triangle in the triangle ABC, where the sum of the interior angles is \[180^\circ \] and then use the central angle theorem to find the required values.

Complete step by step answer:

We are given that the O is the center of the circle, \[{\text{BA}} = {\text{AC}}\] and \[\angle {\text{ABC}} = 50^\circ \].
Joining BC in the given diagram, we get

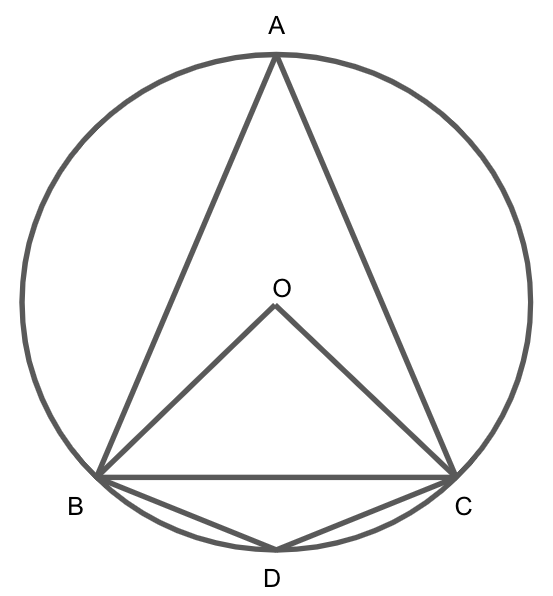
First, we will consider triangle \[\Delta {\text{ABC}}\].
We are given that \[{\text{BA}} = {\text{AC}}\], it means that triangle ABC is an isosceles triangle.
We know that in an isosceles triangle, the two angles inclined on equal and non-equal lines are the same.
\[
   \Rightarrow \angle {\text{ABC}} = \angle {\text{ACB}} \\
   \Rightarrow \angle {\text{ABC}} = 50^\circ \\
 \]
Then we will use the angle sum property of triangle in the triangle ABC, where the sum of the interior angles is \[180^\circ \], we get
\[ \Rightarrow \angle {\text{ABC}} + \angle {\text{ACB}} + \angle {\text{BAC}} = 180^\circ \]
Substituting the value of \[\angle {\text{ABC}}\] and \[\angle {\text{ACB}}\] in the above equation, we get
\[
   \Rightarrow 50^\circ + 50^\circ + \angle {\text{BAC}} = 180^\circ \\
   \Rightarrow 100^\circ + \angle {\text{BAC}} = 180^\circ \\
 \]
Subtracting the above equation by \[100^\circ \] on both sides, we get
\[
   \Rightarrow 100^\circ + \angle {\text{BAC}} - 100^\circ = 180^\circ - 100^\circ \\
   \Rightarrow \angle {\text{BAC}} = 80^\circ \\
 \]
Now according to the central angle theorem, the central angle from any two points on the circle is always twice the inscribed angles from those two points, so we have
\[
   \Rightarrow \angle {\text{BOC}} = 2 \times \angle {\text{BAC}} \\
   \Rightarrow \angle {\text{BOC}} = 2 \times 80^\circ \\
   \Rightarrow \angle {\text{BOC}} = 160^\circ \\
 \]
Using the central angle theorem again, we get
\[
   \Rightarrow \angle {\text{BOC}} = 2 \times \angle {\text{BDC}} \\
   \Rightarrow 160^\circ = 2 \times \angle {\text{BDC}} \\
 \]
Dividing the above equation by 2 on both sides, we get
\[
   \Rightarrow \dfrac{{160^\circ }}{2} = \dfrac{{2 \times \angle {\text{BDC}}}}{2} \\
   \Rightarrow 80^\circ = \angle {\text{BDC}} \\
   \Rightarrow \angle {\text{BDC}} = 80^\circ \\
 \]
Therefore, the measure of \[\angle {\text{BOC}}\] is \[160^\circ \] and \[\angle {\text{BDC}}\] is \[80^\circ \].

Note: In solving these types of questions, you should be familiar with the concept of angle of elevation and the tangential properties. Students should not use any other trigonometric functions like sine or cosine of the given angle because the given condition of the problem, which is provided to us, is of the height of the triangle and a base. So, do not take the sum equal to \[90^\circ \] instead \[180^\circ \], which is wrong.