Question

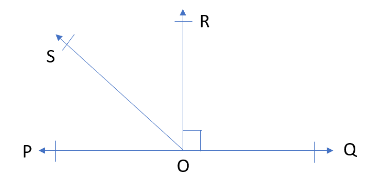
In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
$\angle ROS = \dfrac{1}{2}(\angle QOS - \angle POS).$

Answer 1

Hint: To solve this question, we have been given a figure, where, $\angle ROQ = 90^\circ $ and $\angle ROP = 90^\circ $ then, on keeping $\angle ROP$ and $\angle ROQ$ equal, because the angles are equals to \[90^\circ ,\] then solving further we will get the required expression.

Complete step-by-step answer:
We have been given a figure, in it POQ is a line. We have also been given that the ray OR is perpendicular to line PQ. And, OS is another ray lying between rays OP and OR. We need to prove that $\angle ROS = \dfrac{1}{2}(\angle QOS - \angle POS).$
So, it is given that ray OR is perpendicular to line PQ, i.e., $OR \bot PQ$
From the figure we get that, $\angle ROP = 90^\circ $ and $\angle ROQ = 90^\circ $
So, we can put, $\angle ROP = \angle ROQ$ (because both the angles are equals to \[90^\circ \])
Since, it is given that OS is another ray lying between rays OP and OR.
$ \Rightarrow \angle ROP = \angle POS + \angle ROS$
Now, on putting, $\angle ROQ$in place of $\angle ROP$, because both the angles are equal to each other, we get
$\angle POS + \angle ROS = \angle ROQ$
Since in the question, it is given that, ray OR is perpendicular to line PQ.
$ \Rightarrow \angle POS + \angle ROS = \angle QOS - \angle ROS$
Now, on rearranging the above equation, we get
$2\angle ROS = \angle QOS - \angle POS$
$ \Rightarrow \angle ROS = \dfrac{1}{2}\angle QOS - \angle POS$
Hence proved, $\angle ROS = \dfrac{1}{2}(\angle QOS - \angle POS).$

Note: Before solving, students should carefully observe the given figure. And then using the given information, solve further. To solve these types of question, where we are supposed to prove something, it is usually advisable to start with one side i.e., either start from L.H.S or R.H.S., then eventually we can prove the equation.