Question

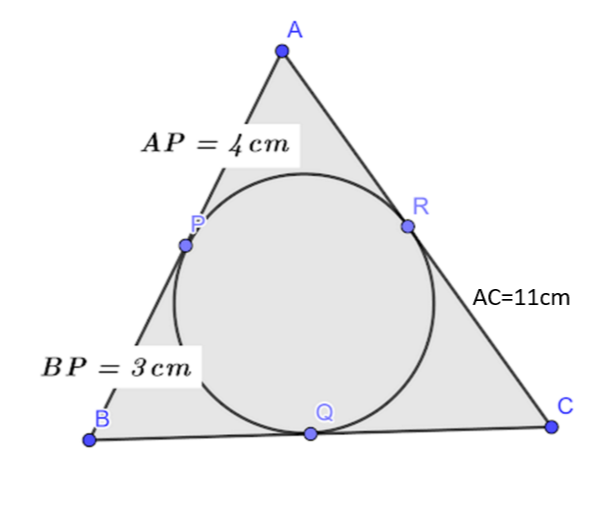
In the figure, the sides AB, BC, and CA of a triangle ABC, touch a circle at P, Q, and R respectively. If PA=4cm, BP=3cm, and AC=11cm, then find the length of BC(in cm).

Answer 1

Hint: We will use the property of a circle that states that the lengths of two tangents from an external point to a circle are equal. To find the length of BC, we will find BQ and QC. We will find BQ with the help of BP and QC with the help of RC. RC can be found by subtracting AR from AC, and AR can be found by PA.
\[\begin{align}
  & BC=BQ+QC \\
 & =3+7 \\
 & BC=10cm \\
\end{align}\]

Complete step-by-step solution:
It is given that sides AB, BC, and CA touch the circle at P, Q, and R respectively. This implies that AB, BC, and CA work as tangents for the circle.
It is given,
\[\begin{align}
  & PA=4cm--(i) \\
 & BP=3cm--(ii) \\
 & AC=11cm--(iii) \\
\end{align}\]
We know that the length of two tangents from an external point to a circle are equal. -----(iv)
From an external point A, PA and RA are tangents to the circle.
From (iv),
\[\begin{align}
  & PA=RA \\
 & \therefore RA=4cm \\
\end{align}\] ---------From (i)
From (iii),
\[\begin{align}
  & AC=11cm \\
 & \Rightarrow AR+RC=11cm \\
 & \Rightarrow 4+RC=11 \\
 & \Rightarrow RC=11-4=7cm \\
\end{align}\]
From an external point B, PB and BQ are tangents to the circle.
From (iv),
PB=BQ
From (ii) BQ=3cm ---------(v)
Now, from an external point C, RC and QC are tangents to the circle.
From (iv),
\[\begin{align}
  & RC=QC \\
 & \therefore QC=7cm--(vi) \\
\end{align}\]
Now,
\[\begin{align}
  & BC=BQ+QC \\
 & =3+7 \\
 & BC=10cm \\
\end{align}\] ------------(from (v),(vi))
Hence, the length of BC is 10cm.

Note: It is necessary to know and learn all the prosperities of a circle. Then we can identify the property which will help us in sorting the given question. Once identified, we should also know the correct application of the property. The best way to do this is to identify and practice all the similar types of questions related to it.