Question

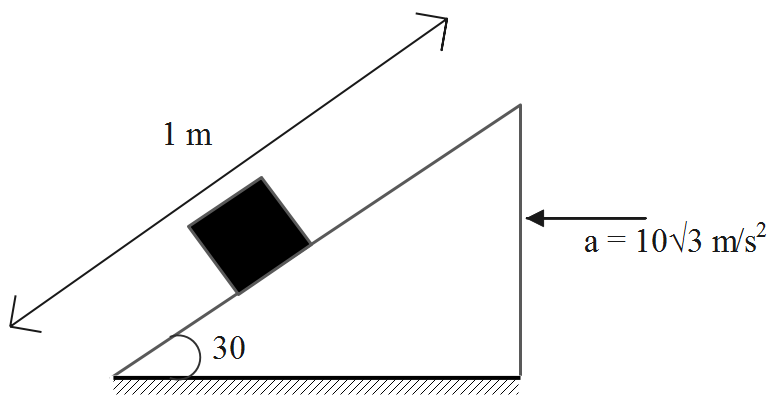
In the figure, the wedge is pushed with an acceleration of \[10\sqrt{3}{m}/{{{s}^{2}}}\;\]. It is seen that the block starts climbing up on the smooth inclined face of the wedge. What will be the time taken by the block to reach the top?

Answer 1

Hint: The acceleration of a body equals the force applied on the body by the mass of that body. The acceleration of the body inclined along the plane equals the ratio of the difference of the product of mass, acceleration and the cosine of angle the product of mass, acceleration due to gravity and the sine of angle and the mass.
Formula used:
\[\begin{align}
  & {{a}_{eff}}=\dfrac{F}{m} \\
 & {{a}_{eff}}=\dfrac{ma\cos \theta -mg\sin \theta }{m} \\
\end{align}\]

Complete step by step answer:
From the given information, we have the data as follows.
The wedge is pushed with an acceleration of \[10\sqrt{3}{m}/{{{s}^{2}}}\;\]. The block starts climbing up on the smooth inclined face of the wedge.
As the block starts climbing up on the smooth inclined face of the wedge, thus, there will be no frictional force acting on the block.
The acceleration equals the force by the mass.
\[{{a}_{eff}}=\dfrac{F}{m}\]
Here, the force equals the ratio of the difference of the product of mass, acceleration and the cosine of angle, the product of mass, acceleration due to gravity and the sine of angle and the mass.
\[{{a}_{eff}}=\dfrac{ma\cos \theta -mg\sin \theta }{m}\]
Substitute the values of the mass, acceleration, the acceleration due to gravity and the angle in the above equation to compute the effective acceleration.
\[\begin{align}
  & {{a}_{eff}}=\dfrac{ma\cos \theta -mg\sin \theta }{m} \\
 & \Rightarrow {{a}_{eff}}=a\cos \theta -g\sin \theta \\
 & \therefore {{a}_{eff}}=10\sqrt{3}\cos 30{}^\circ -10\sin 30{}^\circ \\
\end{align}\]
Continue further computation.
\[\begin{align}
  & {{a}_{eff}}=10\sqrt{3}\cos 30{}^\circ -10\sin 30{}^\circ \\
 & \Rightarrow {{a}_{eff}}=10\sqrt{3}\times \dfrac{\sqrt{3}}{2}-10\times \dfrac{1}{2} \\
 & \Rightarrow {{a}_{eff}}=15-5 \\
 & \therefore {{a}_{eff}}=10{m}/{{{s}^{2}}}\; \\
\end{align}\]
The time taken is,
\[t=\sqrt{\dfrac{2s}{{{a}_{eff}}}}\]
Substitute the values in the above formula.
\[t=\sqrt{\dfrac{2\times 1}{10}}\]
Therefore, the value of the time is,
\[t=\dfrac{1}{\sqrt{5}}s\]
\[\therefore \] The time taken by the block to reach the top is,\[\dfrac{1}{\sqrt{5}}s\].

Note: The units of the parameters should be taken care of. Many times, the values of the parameters will be given in the statements of the question, whereas, in this case, the values of the parameters, such as, the distance is given in the diagram.