Question

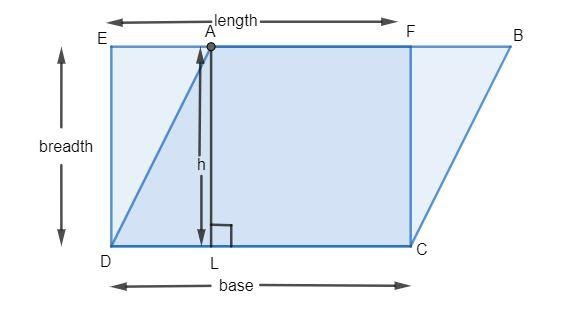
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, \[AL \bot DC\]. Prove that
A) \[{\rm{ar}}\left( {ABCD} \right) = {\rm{ar}}\left( {EFCD} \right)\]
B) \[{\rm{ar}}\left( {ABCD} \right) = DC \times AL\]

Answer 1

Hint:
We will first find the area of the parallelogram using the formula for the area of a parallelogram. Then we will find the area of the rectangle using the formula for the area of a rectangle. We will compare both the areas to prove that both the areas are equal.

Formulas used: We will use the following formulas:
1) The area of a rectangle \[{A_r} = l \times b\], where \[l\] is the length and \[b\] is the base.
2) The area of a parallelogram, \[{A_p} = b \times h\] , where \[h\] is the height and \[b\] is the base.

Complete step by step solution:
We will first prove the \[{\rm{ar}}\left( {ABCD} \right) = DC \times AL\].
(ii) We will find the area of parallelogram ABCD. We know that the area of a parallelogram is the product of the length of its height and base. So, we can write
\[ar\left( {ABCD} \right) = b \times h\]
The height of a parallelogram is the perpendicular distance between its 2 parallel opposite sides and the base of the parallelogram is its lowermost side. We can see from the figure that the height of the parallelogram is \[AL\] and the base is \[DC\]. We will substitute these values in the formula for the area of a parallelogram:
\[ \Rightarrow ar\left( {ABCD} \right) = AL \times DC\]
Hence, we have proved \[{\rm{ar}}\left( {ABCD} \right) = DC \times AL\].
Now, we will prove the \[{\rm{ar}}\left( {ABCD} \right) = {\rm{ar}}\left( {EFCD} \right)\].
We will find the area of the rectangle EFCD. We know that the area of a rectangle is its length times breadth.
\[ \Rightarrow ar\left( {EFCD} \right) = {\rm{length}} \times {\rm{breadth}}\]
Usually, the longer side of a rectangle is taken as its length and the shorter side is taken as its breadth. The breadth of a rectangle is always perpendicular to its length just like the height of a parallelogram. We can see from the figure that the length of the rectangle is \[EF\] and the breadth is \[ED\]. We will substitute these values in the formula for the area of a rectangle.
Therefore,
\[ \Rightarrow ar\left( {EFCD} \right) = EF \times ED\]
We know that the opposite sides of a rectangle are equal in length. So,
\[EF = DC\]
We can see from the figure that the breadth of the rectangle and the height of the parallelogram are equal. So, we can write
\[ED = AL\]
So, the area of rectangle EFCD can be rewritten as:
\[ \Rightarrow ar\left( {EFCD} \right) = DC \times AL\]
We know that the area of parallelogram ABCD is also \[AL \times DC\].

$\therefore ar\left( ABCD \right)=ar\left( EFCD \right)$

Note:
A parallelogram is a quadrilateral whose opposite sides are parallel and equal. A rectangle is a special kind of parallelogram with all its angles as right angles. The area of a rectangle is also the same as the area of a parallelogram as the base of the parallelogram is the rectangle’s length and the height of the parallelogram is the rectangle’s breadth.