Question

In the following figure, $ABCD$ is a parallelogram in which $\angle BAO={{35}^{\circ }},\angle DAO={{40}^{\circ }}$ and $\angle COD={{105}^{\circ }}$.

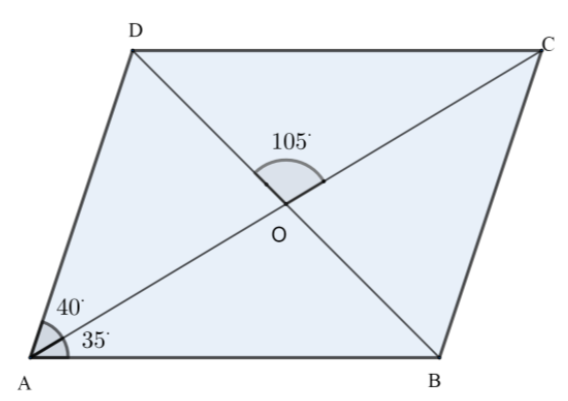
Calculate the following angles:
A. $\angle ABO$
B. $\angle ODC$
C. $\angle ACB$
D. $\angle CBD$

Answer 1

Hint: First we will look at the figure and analyze that where is the most data are given in the figure so then we will start with $\Delta AOB$ and apply the angle sum property for this we need to know at least two angles in order to find the third so we will apply vertical opposite angles property on $\angle COD$ and through that, we will find our first option that is $\angle ABO$ similarly, we will apply the angle sum property on triangle BCD and ABC and find answers for our options B and C. For option D we will apply the parallelogram property that adjacent angles are supplementary.

Complete step-by-step solution:
It is given that $ABCD$ is a parallelogram having $\angle BAO={{35}^{\circ }},\angle DAO={{40}^{\circ }}$ and $\angle COD={{105}^{\circ }}$.
Now, we know that vertically opposite angles are equal. Therefore, $\angle COD=\angle AOB={{105}^{\circ }}$.
So, in $\Delta AOB$ , by angle sum property of triangle which states that the sum of all the three angle is ${{180}^{\circ }}$. Therefore:
$\begin{align}
  & \Rightarrow \angle AOB+\angle OAB+\angle ABO={{180}^{\circ }} \\
 & \Rightarrow {{105}^{\circ }}+{{35}^{\circ }}+\angle ABO={{180}^{\circ }} \\
 & \Rightarrow \angle ABO={{40}^{\circ }} \\
\end{align}$
Therefore, the answer of A : $\angle ABO={{40}^{\circ }}$
Now, we know that adjacent angles of a parallelogram are supplementary means there sum is: ${{180}^{\circ }}$ ,Therefore: $\angle DAB+\angle ABC={{180}^{\circ }}$
Now we know from the figure that:
$\begin{align}
  & \angle DAB=\angle DAO+\angle OAB \\
 & \angle ABC=\angle ABO+\angle CBO \\
\end{align}$
We will now put these values in $\angle DAB+\angle ABC={{180}^{\circ }}$
$\begin{align}
  & \Rightarrow \angle DAO+\angle OAB+\angle ABO+\angle CBO={{180}^{\circ }} \\
 & \Rightarrow {{40}^{\circ }}+{{35}^{\circ }}+{{40}^{\circ }}+\angle CBO={{180}^{\circ }} \\
 & \Rightarrow \angle CBO={{180}^{\circ }}-{{115}^{\circ }}={{65}^{\circ }} \\
\end{align}$
Now, we can see in the figure that: $\angle CBO=\angle CBD={{65}^{\circ }}$ .
Therefore, the answer for D is $\angle CBD={{65}^{\circ }}$.
Again we see that in $\Delta ABC$ , by angle sum property of triangle which states that the sum of all the three angle is ${{180}^{\circ }}$. Therefore: $\angle CAB+\angle ABC+\angle ACB={{180}^{\circ }}$
 Now we know from the figure that: $\angle ABC=\angle ABO+\angle CBO$
Therefore,
 \[\begin{align}
  & \Rightarrow {{35}^{\circ }}+\angle ABO+\angle CBO+\angle ACB={{180}^{\circ }} \\
 & \Rightarrow {{35}^{\circ }}+{{40}^{\circ }}+{{65}^{\circ }}+\angle ACB={{180}^{\circ }} \\
 & \Rightarrow \angle ACB={{180}^{\circ }}-{{140}^{\circ }}={{40}^{\circ }} \\
\end{align}\]
Therefore, the answer for C is $\angle ACB={{40}^{\circ }}$.
Now we know that the opposite angles of a parallelogram are equal, therefore:
 \[\begin{align}
  & \angle A=\angle C \\
 & \Rightarrow {{35}^{\circ }}+{{40}^{\circ }}=\angle C \\
 & \Rightarrow \angle C={{75}^{\circ }} \\
\end{align}\]
We will now apply the angle sum property of triangle in $\Delta BCD$, we will get
$\begin{align}
  & \angle C+\angle CBD+\angle CDB={{180}^{\circ }} \\
 & \Rightarrow {{75}^{\circ }}+{{65}^{\circ }}+\angle CDB={{180}^{\circ }} \\
 & \Rightarrow \angle CDB={{40}^{\circ }} \\
\end{align}$
Now, we can see in the figure that: $\angle CBO=\angle CBD={{65}^{\circ }}$ .
Therefore, the answer for D is $\angle CBD={{65}^{\circ }}$.
Now, we can see in the figure that: $\angle CDB=\angle ODC={{40}^{\circ }}$ .
Therefore, the answer for B is $\angle ODC={{40}^{\circ }}$.
So we have found out all the angles as asked:
A. $\angle ABO={{40}^{\circ }}$
B. $\angle ODC={{40}^{\circ }}$
C. $\angle ACB={{40}^{\circ }}$
D. $\angle CBD={{65}^{\circ }}$

Note: A misconception that student may have like $\angle A+\angle D={{360}^{\circ }}$ instead of ${{180}^{\circ }}$. Remember that the supplementary angle means that the sum is ${{180}^{\circ }}$ whereas the complementary angles mean that their measures add to ${{90}^{\circ }}$. Always draw the figure in such cases as it is easier for the student to write the solution as well as for the examiner to understand it.