Question

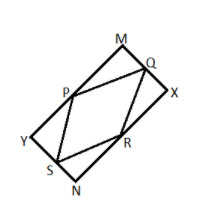
In the following figure PQRS is a rhombus formed by joining the midpoints of a quadrilateral YMXN show that $3P{Q^2} = S{N^2} + N{R^2} + Q{X^2} + X{R^2} + P{Y^2} + Y{S^2}$

Answer 1

Hint: In this particular question use the concept that in a rhombus all the side lengths are equal and the adjacent sides w.r.t the particular sides of the given quadrilateral are perpendicular to each other and later on in the solution use the concept of Pythagoras theorem so use these concepts to reach the solution of the question.

Complete step-by-step answer:
Proof –
As we see from the figure that in the given quadrilateral YMXN the adjacent sides are perpendicular to each other and opposite sides are parallel to each other but the adjacent side lengths are unequal.
So YMXN is a rectangle.
Now it is given that PQRS is a rhombus.
As we know that in a rhombus all the side lengths are equal.
Therefore, PQ = QR = RS = SP................. (1)
Now all the four triangles formed by the sides of the rhombus PQRS and the rectangle as shown in the figure are right angles.
So according to Pythagoras theorem, Hypotenuse square is equal to the sum of the square of base and perpendicular so we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
Now in right angle triangle PSY we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {{\text{SP}}} \right)^2} = {\left( {{\text{YS}}} \right)^2} + {\left( {PY} \right)^2}$.................. (2)
Now in right angle triangle SNR we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {{\text{RS}}} \right)^2} = {\left( {{\text{SN}}} \right)^2} + {\left( {{\text{NR}}} \right)^2}$.................. (3)
Now in right angle triangle RXQ we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {{\text{QR}}} \right)^2} = {\left( {{\text{QX}}} \right)^2} + {\left( {XR} \right)^2}$.................. (4)
Now add equation (2), (3) and (4) we have,
$ \Rightarrow {\left( {{\text{SP}}} \right)^2} + {\left( {{\text{RS}}} \right)^2} + {\left( {{\text{QR}}} \right)^2} = {\left( {{\text{YS}}} \right)^2} + {\left( {PY} \right)^2} + {\left( {{\text{SN}}} \right)^2} + {\left( {{\text{NR}}} \right)^2} + {\left( {{\text{QX}}} \right)^2} + {\left( {XR} \right)^2}$
Now from equation (1), PQ = QR = RS = SP we have,
$ \Rightarrow {\left( {{\text{PQ}}} \right)^2} + {\left( {{\text{PQ}}} \right)^2} + {\left( {{\text{PQ}}} \right)^2} = {\left( {{\text{YS}}} \right)^2} + {\left( {PY} \right)^2} + {\left( {{\text{SN}}} \right)^2} + {\left( {{\text{NR}}} \right)^2} + {\left( {{\text{QX}}} \right)^2} + {\left( {XR} \right)^2}$
$ \Rightarrow 3{\left( {{\text{PQ}}} \right)^2} = {\left( {{\text{YS}}} \right)^2} + {\left( {PY} \right)^2} + {\left( {{\text{SN}}} \right)^2} + {\left( {{\text{NR}}} \right)^2} + {\left( {{\text{QX}}} \right)^2} + {\left( {XR} \right)^2}$
Hence proved.

Note: Whenever we face such types of questions the key concept we have to remember is the Pythagoras theorem which is Hypotenuse square is equal to the sum of the square of base and perpendicular so apply this in all of the triangles except PMQ as above and add them we will get the required answer.