Question

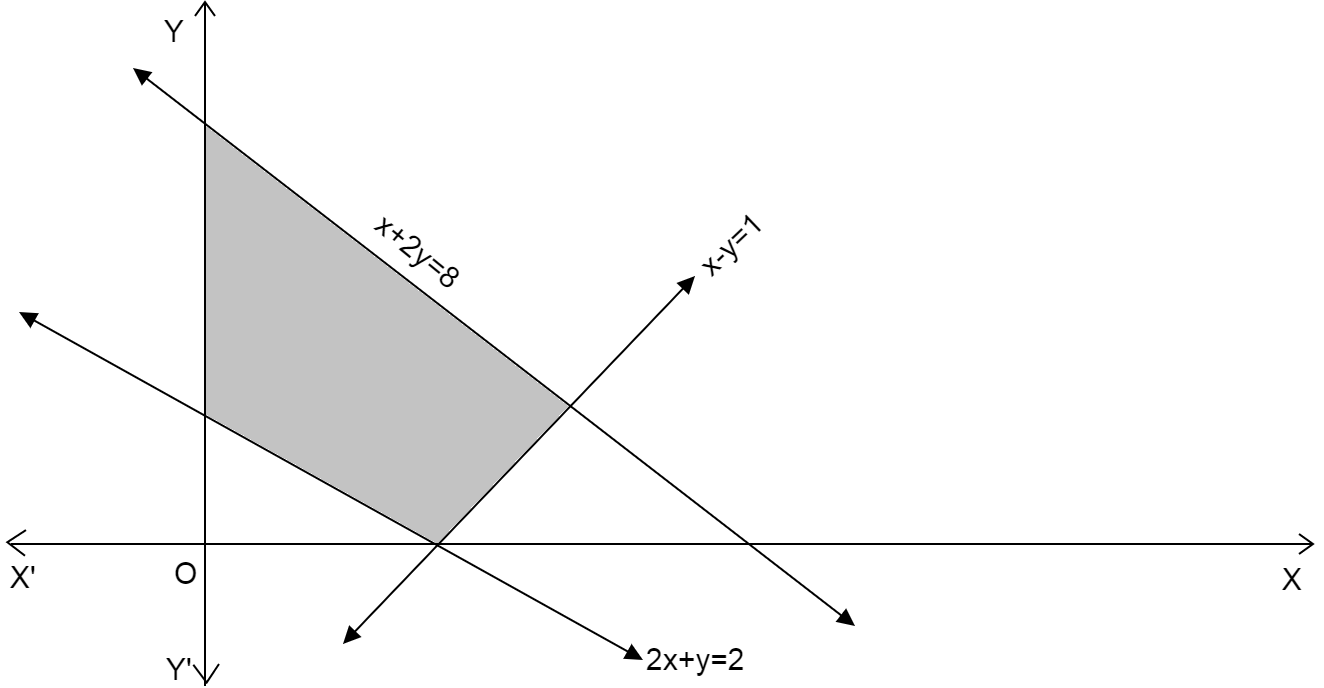
In the following shaded region, the linear constraints (except \[x \geqslant 0\]and\[y \geqslant 0\]) are:

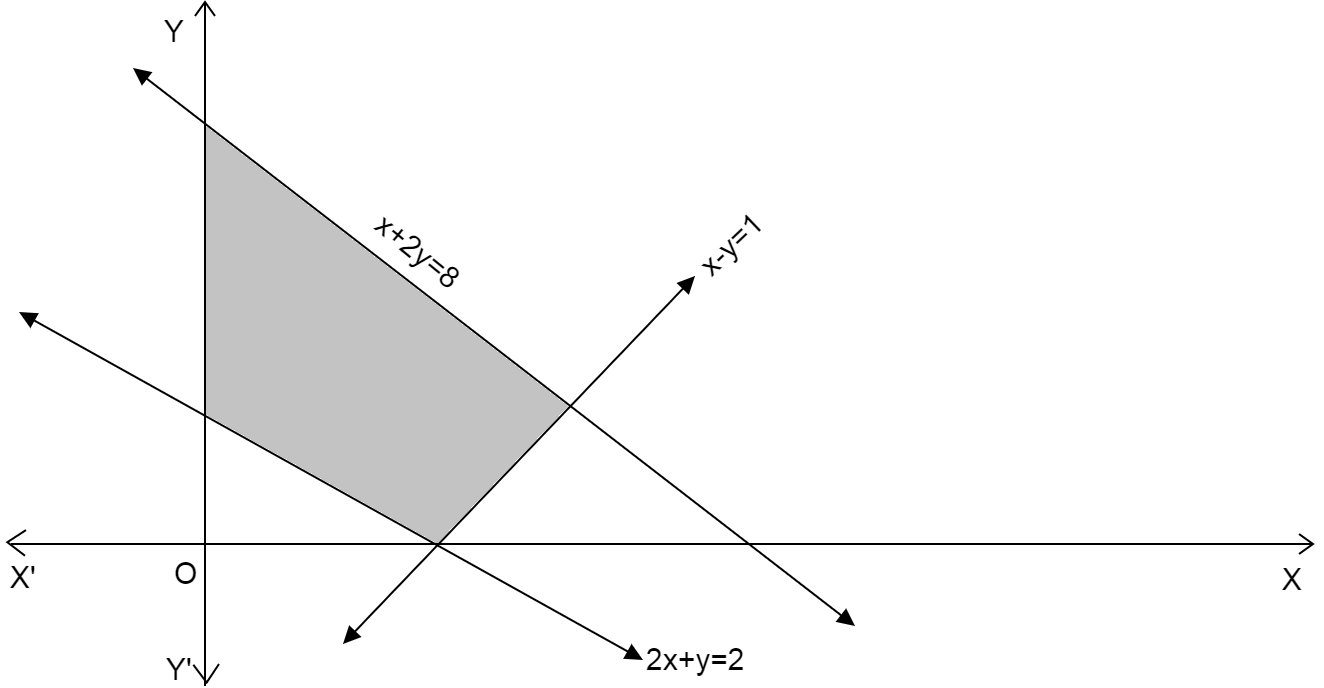
A.\[2x + y \leqslant 2,x - y \leqslant 1,x + 2y \leqslant 8\]
B.\[2x + y \geqslant 2,x - y \leqslant 1,x + 2y \leqslant 8\]
C.\[2x + y \leqslant 2,x - y \geqslant 1,x + 2y \leqslant 8\]
D.\[2x + y \leqslant 2,x - y \leqslant 1,x + 2y \geqslant 8\]

Answer 1

Hint: We use the concept of shading a region between the equations by comparing the signs ‘less than equal to (\[ \leqslant \])’ and ‘greater than equal to (\[ \geqslant \])’ between the equation and the constant value on the other side of the equation. Check the sign of inequality for each equation and choose the option that holds true for all the three equations.
* If the equation of the straight line is less than or equal to a constant, then shade the area below the line.
* If the equation of the straight line is greater than or equal to a constant then shade the area above the line.

Complete step by step answer:
We are given the figure where there are three straight lines \[2x + y = 2;x - y = 1;x + y = 8\]
The three straight lines intersect each other at some point and intersect the x-axis and y-axis.
The shaded region is in the first quadrant where both x coordinate and y coordinate are positive.

We have constraints \[x \geqslant 0\]and\[y \geqslant 0\]
We look at each line separately and check the inequality by considering a point.
First:
We consider the line \[x + 2y = 8\]
Since, the shaded region in the graph is below the line \[x + 2y = 8\]
We take the inequality \[x + 2y \leqslant 8\]
Check the inequality by considering a point.
Let \[(0,0)\]be the point. Since this point lies below the line it must satisfy the inequality.
\[ \Rightarrow (0) + 2(0) \leqslant 8\]
\[ \Rightarrow 0 \leqslant 8\]
Therefore the inequality for the line \[x + 2y = 8\] that represents the shaded region is \[x + 2y \leqslant 8\].
Second:
We consider the line \[x - y = 1\]
Since the shaded region in the graph is above the line \[x - y = 1\]
We take the inequality \[x - y \geqslant 1\]
Check the inequality by considering a point.
Let \[(0,0)\]be the point. Since this point lies above the line it must satisfy the inequality.
\[ \Rightarrow (0) - (0) \geqslant 1\]
\[ \Rightarrow 0 \geqslant 1\]
This is incorrect as the point above the line does not satisfy the inequality.
So we take the inequality \[x - y \leqslant 1\]
Therefore the inequality for the line \[x - y = 1\] that represents the shaded region is \[x - y \leqslant 1\].
Third:
We consider the line \[2x + y = 2\]
Since the shaded region in the graph is above the line \[2x + y = 2\]
We take the inequality \[2x + y \geqslant 2\]
Check the inequality by considering a point.
Let \[(1,1)\] be the point. Since this point lies above the line it must satisfy the inequality.
\[ \Rightarrow 2(1) + (1) \geqslant 2\]
\[ \Rightarrow 3 \geqslant 2\]
Therefore the inequality for the line \[2x + y = 2\] that represents the shaded region is \[2x + y \geqslant 2\].
From the three cases we get the set of constraints as: \[x + 2y \leqslant 8\]; \[x - y \leqslant 1\] and \[2x + y \geqslant 2\].

\[\therefore \] Option (B) is the correct option.

Note:
Students might get confused with the shaded region as it depicts the inequality \[x - y \geqslant 1\] for the line \[x - y = 1\]. Keep in mind, we always check if the inequality holds true or not by considering a point above or below the line which should give the required result.
Also, many students try to find the points of intersections of three lines and then check the shaded region, this process is long and we have no use of points of intersection of lines in this solution.