Question

In the game of chess, the Knight can make any of the moves displayed in the diagram to the right. If a Knight is the only piece on the board, what is the greatest number of spaces from which not all 8 moves are possible?

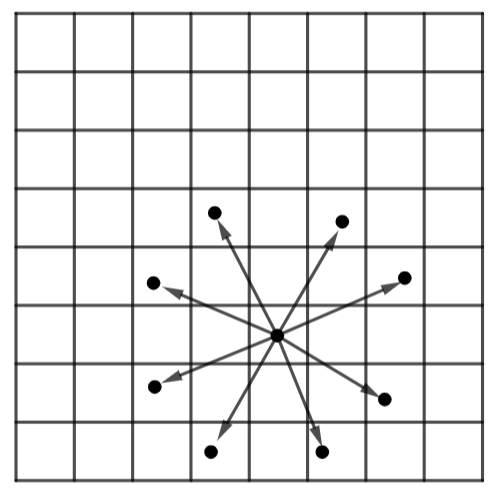
(a) 8
(b) 24
(c) 38
(d) 48

Answer 1

Hint: To solve the given question we will treat the chessboard as a square matrix with 8 rows and 8 columns. Now, we will use the fact that if not all 8 moves are possible for the knight then it should be present in the first or the second or the seventh or the eighth row or column. Thus, we will count the number of elements in these rows or columns and that will be equal to the number of cases when all 8 moves are not possible.
Complete step by step solution:
To start with we will assume the chessboard as a square matrix with 8 rows and 8 columns. Now, we have to find the total number of positions at which the knight is present and all 8 moves are not possible. We can see that when the knight is present in the first row or the second row, all 8 moves are not possible. Similarly, when it is present in the seventh row or the eighth row, all 8 moves are not possible. Thus, there are four rows at which knights should be present to fulfill the condition of the question. We know that there are 8 elements in each row. So, the total number of positions $$=8\times 4=32.$$
Now, similarly, the knight can be present in the first two columns and last two columns, so that all 8 moves are not possible. So, there are 4 columns at which knights should be present to fulfill the condition of the question. Now there are 8 elements in each column. So, the total number of positions $$=8\times 4+32.$$
Now, when we have taken the first two rows of the first two columns, 4 positions are common. When the first two rows and last two columns are taken, 4 positions are common. When the first two columns and the last two rows are taken, 4 positions are common. When the last two rows and the last two columns are taken, 4 positions are common. These cases need to be subtracted from the total positions. Thus, we will get,
Required number of positions = 32 + 32 – (4 + 4 + 4 + 4)
Therefore, required number of positions = 64 – 16 = 48
Thus, there are 48 positions at which the knight is present such that all 8 moves are not possible.

Note: We can count the number of positions alternately also. For this, we will first count the number of positions at which all 8 moves are possible. The number of positions at which all 8 moves are possible is the $$4\times 4$$ inner square matrix. The number of elements in this matrix is $$4\times 4=16.$$ The total number of positions in the matrix are $$8\times 8=64.$$
Required positions = Total – (Positions at which total 8 moves are possible)
Therefore, the required positions = 64 – 16 = 48