
In the game of see-saw, what should be the displacement of the boy B from the right edge to keep see-saw in equilibrium? (
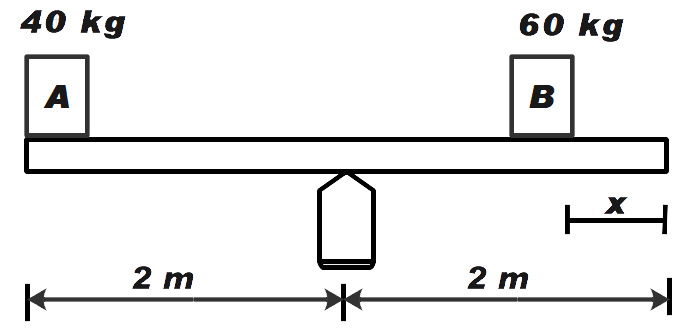
A.
B. 1 m
C.
D. zero

Answer
495.6k+ views
Hint: In this question, we have been asked to calculate the distance of boy B from the right edge. We know that see-saw works on the principle of lever and fulcrum. The lever moves the object with fulcrum because of the torque applied on the end of fulcrum. So to maintain the see-saw in equilibrium we need to balance the torque.
Formula used:
Where,
Complete step by step answer:
From the figure given, we can say that torque at point O should be zero. This is a necessary condition for the see-saw to be in equilibrium. In terms of equation we can write it as
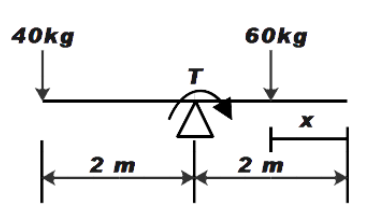
We know that Torque is the product of magnitude of force and perpendicular distance of the line of action of force.
Let us consider that, boy B is sitting at distance x from the right edge. Therefore, the distance of boy B from centre point O will be (2-x). Now, considering the positive X-axis as positive direction for distance and point O as the origin
We can say
On solving
We get,
Therefore,
So, in order to maintain the equilibrium for the see-saw boy B must sit distance
So, the correct answer is “Option C”.
Note: The force that causes the object to rotate about an axis is called the Torque. Torque causes the object to gain angular acceleration. The SI unit of torque is Newton metre (Nm). Torque in rotational motion is basically the same as force in linear motion. It depends on the amount of force applied and the perpendicular distance from the axis of rotation to point of force applied.
Formula used:
Where,
Complete step by step answer:
From the figure given, we can say that torque at point O should be zero. This is a necessary condition for the see-saw to be in equilibrium. In terms of equation we can write it as

We know that Torque is the product of magnitude of force and perpendicular distance of the line of action of force.
Let us consider that, boy B is sitting at distance x from the right edge. Therefore, the distance of boy B from centre point O will be (2-x). Now, considering the positive X-axis as positive direction for distance and point O as the origin
We can say
On solving
We get,
Therefore,
So, in order to maintain the equilibrium for the see-saw boy B must sit distance
So, the correct answer is “Option C”.
Note: The force that causes the object to rotate about an axis is called the Torque. Torque causes the object to gain angular acceleration. The SI unit of torque is Newton metre (Nm). Torque in rotational motion is basically the same as force in linear motion. It depends on the amount of force applied and the perpendicular distance from the axis of rotation to point of force applied.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




