Question

In the given figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7, find the area of the shaded region.

Answer 1

Hint – In this question we have to find the area of the shaded region, so using the concept that if the smaller circle area is removed from the larger circle’s area then eventually the only left area is the required shaded region.

Complete step-by-step answer:
As we know that the area (A) of the circle is $\pi {r^2}$ (where r is the radius of the small circle).
Now as we know that diameter (d) of a circle is twice the radius.
$
   \Rightarrow d = 2r \\
   \Rightarrow r = \dfrac{d}{2} \\
$
So substitute this value in the formula of area of small circle we have
$ \Rightarrow A = \pi {\left( {\dfrac{d}{2}} \right)^2} = \pi \dfrac{{{d^2}}}{4}$……………… (1)
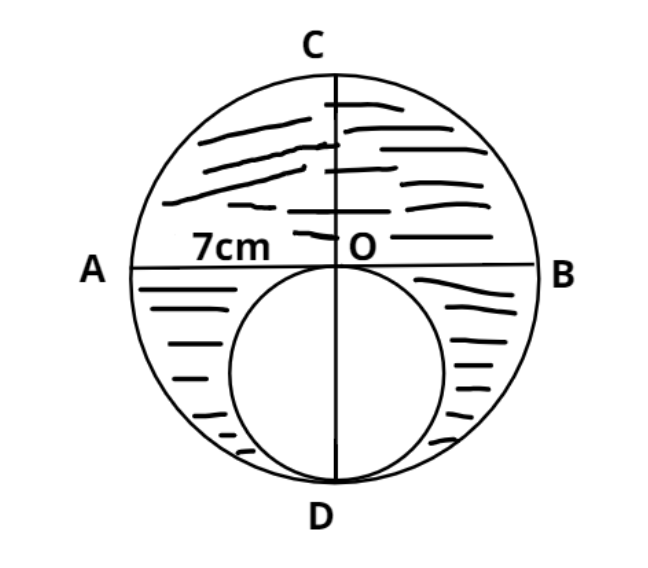
Now it is given that AB and CD are the two diameters of a circle perpendicular to each other.
$ \Rightarrow AB = CD$ (Diameter of the circle).
And we know half of the diameter is the radius of the circle.
$ \Rightarrow OA = OB = OC = OD = \dfrac{{AB}}{2} = \dfrac{{CD}}{2}$ (Radius of the circle).
Now it is given that OD = 7 unit and it is the diameter (${d_1}$) of the smaller circle.
So the area (${A_1}$) of the smaller circle from equation (1)
$ \Rightarrow {A_1} = \pi {\left( {\dfrac{{{d_1}}}{2}} \right)^2} = \pi \dfrac{{{d_1}^2}}{4} = \pi \dfrac{{{7^2}}}{4} = \dfrac{{49\pi }}{4}$.
And the diameter (${d_2}$) of the big circle is $\left( {2 \times 7} \right) = 14$ unit.
So the area (${A_2}$) of the big circle is
$ \Rightarrow {A_2} = \pi {\left( {\dfrac{{{d_2}}}{2}} \right)^2} = \pi \dfrac{{{d_2}^2}}{4} = \pi \dfrac{{{{\left( {14} \right)}^2}}}{4} = \dfrac{{196\pi }}{4}$
So the area (${A_3}$) of the shaded portion is
= Area of big circle – area of smaller circle.
$ \Rightarrow {A_3} = \dfrac{{196\pi }}{4} - \dfrac{{49\pi }}{4} = \dfrac{{147\pi }}{4}$
Now substitute $\left[ {\pi = \dfrac{{22}}{7}} \right]$ we have,
$ \Rightarrow {A_3} = \dfrac{{147\pi }}{4} = \dfrac{{147}}{4}\left( {\dfrac{{22}}{7}} \right) = \dfrac{{21 \times 11}}{2} = \dfrac{{231}}{2}$ Sq. units.
So, the area of the shaded portion is $\dfrac{{231}}{2}$ sq. units.
So, this is the required answer.

Note – Whenever we face such types of problems the key concept is simply to have the gist of the basic formula of area of circle and the basics of obtaining radius of circle using diameter. The diagrammatic representation of the figure always helps in better understanding of the geometry involved for the shaded area.