
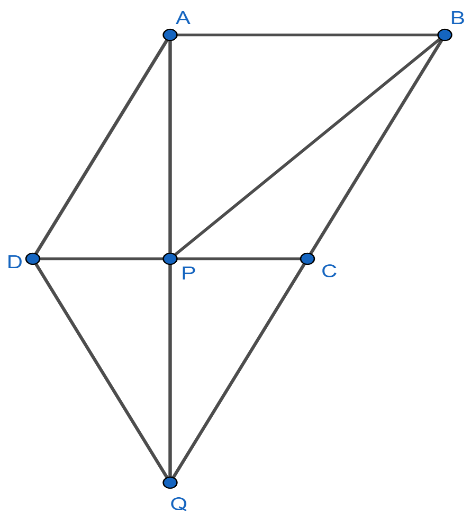
In the given figure $ABCD$ is a parallelogram and $BC$ is produced to a point $Q$ such that $AD=CQ$ . If $AQ$ intersect $DC$ at $P$ , show that $ar\left( BPC \right)=ar\left( DPQ \right)$ .

Answer
609k+ views
Hint: For solving this question first we will see an important property about the median of a triangle that the median of any triangle divides it into two triangles of equal area. Then, we will use the angle side angle property to prove two triangles congruent. Then, we will prove the desired result.
Complete step-by-step answer:
Given:
It is given that $ABCD$ is a parallelogram and $BC$ is produced to a point $Q$ such that $AD=CQ$ and we have to prove that $ar\left( BPC \right)=ar\left( DPQ \right)$ . For more clarity look at the figure given below:
Now, we will have one important property related to the median of the triangles which will be used to solve this problem. The property is that the median of any triangle divides the triangle into two triangles of equal area. For example, consider a $\Delta PQR$ and $PS$ is the median as shown in the figure below:

Now, from the property, we can say that $ar\left( \Delta PQS \right)=ar\left( \Delta PRS \right)$ .
Now, we come back to our problem. As it is given that $ABCD$ is a parallelogram and $AD=CQ$ . Then,
$AD=QC=BC$
Now, consider the $\Delta BPQ$ . From the above equation, we can say that $BC=QC$ . So, $C$ will be the midpoint of the side $BQ$ and $PC$ will be the median of the $\Delta BPQ$ . Then,
$ar\left( BPC \right)=ar\left( \Delta QPC \right)..........\left( 1 \right)$
Now, in $\Delta APD$ and $\Delta QPC$ . We have:
1. $AD=QC$ ( Given).
2. $\angle PAD=\angle PQC$ (Alternate interior angles are equal).
3. $\angle PDA=\angle PCQ$ (Alternate interior angles are equal).
Now, by considering the above 3 points with the help of ASA (Angle Side Angle) congruence rule we conclude that: $\Delta APD\cong \Delta QPC$ . As corresponding sides of congruent triangles are equal in length. Then,
$DP=CP$
Now, consider the $\Delta QDC$ . From the above equation, we can say that $DP=CP$ . So, $P$ will be the midpoint of the side $CD$ and $PQ$ will be the median of the $\Delta BPQ$ . Then,
$ar\left( DPQ \right)=ar\left( \Delta QPC \right)..........\left( 2 \right)$
Now, comparing equation (1) and equation (2). Then,
$ar\left( BPC \right)=ar\left( \Delta QPC \right)=ar\left( DPQ \right)$
Now, from the above result, we can say that $ar\left( BPC \right)=ar\left( DPQ \right)$ .
Hence, proved.
Note: Here, the student must take care of the geometrical properties of the parallelogram and property of the median of a triangle. And proceed in a stepwise manner to prove the result. Moreover, be careful in writing the name of congruent triangles. For example in this question we cannot write that $\Delta ADP\cong \Delta QPC$ , the correct way is $\Delta APD\cong \Delta QPC$
Complete step-by-step answer:
Given:
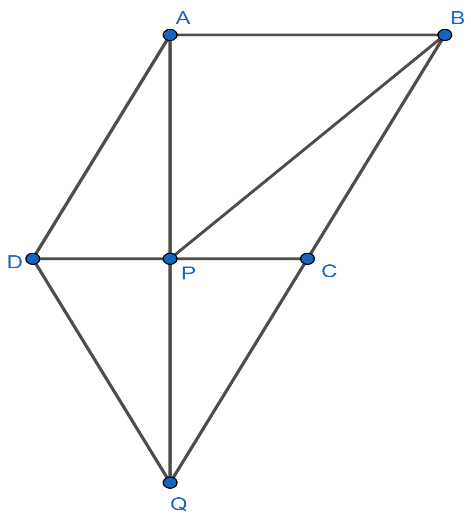
It is given that $ABCD$ is a parallelogram and $BC$ is produced to a point $Q$ such that $AD=CQ$ and we have to prove that $ar\left( BPC \right)=ar\left( DPQ \right)$ . For more clarity look at the figure given below:

Now, we will have one important property related to the median of the triangles which will be used to solve this problem. The property is that the median of any triangle divides the triangle into two triangles of equal area. For example, consider a $\Delta PQR$ and $PS$ is the median as shown in the figure below:

Now, from the property, we can say that $ar\left( \Delta PQS \right)=ar\left( \Delta PRS \right)$ .
Now, we come back to our problem. As it is given that $ABCD$ is a parallelogram and $AD=CQ$ . Then,
$AD=QC=BC$
Now, consider the $\Delta BPQ$ . From the above equation, we can say that $BC=QC$ . So, $C$ will be the midpoint of the side $BQ$ and $PC$ will be the median of the $\Delta BPQ$ . Then,
$ar\left( BPC \right)=ar\left( \Delta QPC \right)..........\left( 1 \right)$
Now, in $\Delta APD$ and $\Delta QPC$ . We have:
1. $AD=QC$ ( Given).
2. $\angle PAD=\angle PQC$ (Alternate interior angles are equal).
3. $\angle PDA=\angle PCQ$ (Alternate interior angles are equal).
Now, by considering the above 3 points with the help of ASA (Angle Side Angle) congruence rule we conclude that: $\Delta APD\cong \Delta QPC$ . As corresponding sides of congruent triangles are equal in length. Then,
$DP=CP$
Now, consider the $\Delta QDC$ . From the above equation, we can say that $DP=CP$ . So, $P$ will be the midpoint of the side $CD$ and $PQ$ will be the median of the $\Delta BPQ$ . Then,
$ar\left( DPQ \right)=ar\left( \Delta QPC \right)..........\left( 2 \right)$
Now, comparing equation (1) and equation (2). Then,
$ar\left( BPC \right)=ar\left( \Delta QPC \right)=ar\left( DPQ \right)$
Now, from the above result, we can say that $ar\left( BPC \right)=ar\left( DPQ \right)$ .
Hence, proved.
Note: Here, the student must take care of the geometrical properties of the parallelogram and property of the median of a triangle. And proceed in a stepwise manner to prove the result. Moreover, be careful in writing the name of congruent triangles. For example in this question we cannot write that $\Delta ADP\cong \Delta QPC$ , the correct way is $\Delta APD\cong \Delta QPC$
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




