
In the given figure,
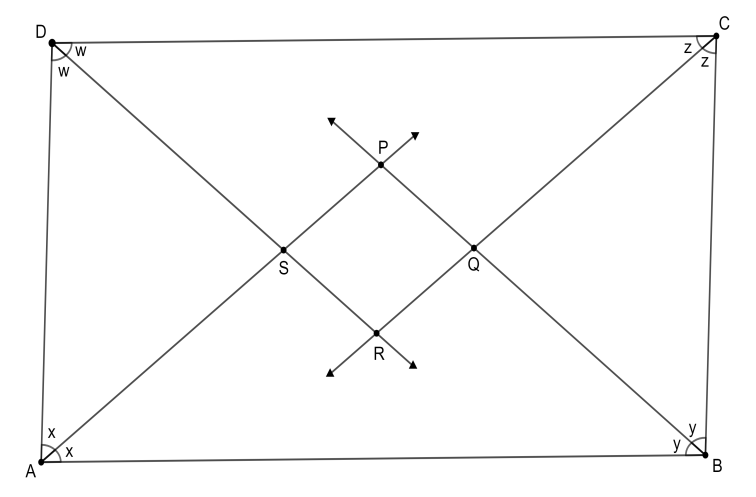
(a) a square
(b) a parallelogram
(c) a rectangle
(d) a rhombus

Answer
500.1k+ views
Hint: We will use the fact that
Complete step-by-step answer:
We know that the adjacent angles of a parallelogram are supplementary. Therefore, we have
Dividing by 2 on both sides of all four equations, we get the following set of equations,
Now, consider
We have already noted that
Similarly, in
Now, we know that opposite angles are congruent. Hence,
Let us consider
Now, considering
As
Now, in quadrilateral
So, the correct answer is “Option C”.
Note: From the given information in the question, we are able to conclude that all the angles of the quadrilateral
Complete step-by-step answer:
We know that the adjacent angles of a parallelogram are supplementary. Therefore, we have
Dividing by 2 on both sides of all four equations, we get the following set of equations,
Now, consider
We have already noted that
Similarly, in
Now, we know that opposite angles are congruent. Hence,
Let us consider
Now, considering
As
Now, in quadrilateral
So, the correct answer is “Option C”.
Note: From the given information in the question, we are able to conclude that all the angles of the quadrilateral
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




