Question

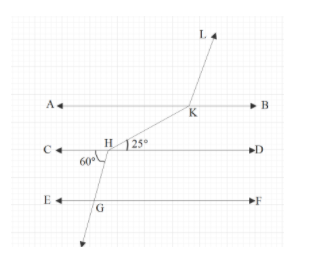
In the given figure $AB\parallel CD\parallel EF$and $GH\parallel KL$, The measure of $\angle HKL$ is

Answer 1

Hint: Extend GH and KL backward. We get the diagram shown below.

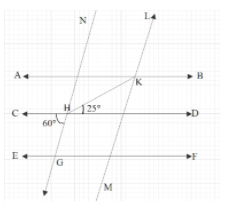
Now find $\angle GHD$ by using the linear pair condition, i.e. sum of angles is ${{180}^{\circ }}$. Then use the result to find $\angle HKM $ by using the co-interior angles condition. Now, again use the linear condition between $\angle HKL$ and $\angle HKM$ to get the value of $\angle HKL$.

Complete step-by-step answer:
Since we have a linear pair of $\angle GHC$ and $\angle GHD$, so by using linear pair condition, we can write:
\[\angle GHC+\angle GHD={{180}^{\circ }}......(1)\]
We have: $\angle GHC={{60}^{\circ }}$
Put the value of $\angle GHC$, we get:
\[\begin{align}
  & \Rightarrow {{60}^{\circ }}+\angle GHD={{180}^{\circ }} \\
 & \Rightarrow \angle GHD={{120}^{\circ }}......(2) \\
\end{align}\]
Now, we have $GN\parallel KM$
Therefore, we can say that, sum of co-interior angles is ${{180}^{\circ }}$.
So, we have:
$\begin{align}
  & \angle GHK+\angle HKM={{180}^{\circ }} \\
 & \angle GHD+\angle DHK+\angle HKM={{180}^{\circ }}......(3) \\
\end{align}$
We have: $\angle DHK={{25}^{\circ }}$
Put the value of $\angle GHD$ and $\angle DHK$ in equation (3), we get:
$\begin{align}
  & \Rightarrow {{120}^{\circ }}+{{25}^{\circ }}+\angle HKM={{180}^{\circ }} \\
 & \Rightarrow \angle HKM={{35}^{\circ }}......(4) \\
\end{align}$
Since we have a linear pair of $\angle HKM$ and$\angle HKL$, so by using linear pair condition, we can write:
\[\angle HKM+\angle HKL={{180}^{\circ }}......(5)\]
We have: $\angle HKM={{35}^{\circ }}$
Put the value of $\angle HKM$, we get:
\[\begin{align}
  & \Rightarrow {{35}^{\circ }}+\angle HKL={{180}^{\circ }} \\
 & \Rightarrow \angle HKL={{145}^{\circ }} \\
\end{align}\]
Hence, $\angle HKL={{145}^{\circ }}$

Note: A linear pair of angles is formed when two lines intersect. Two angles are said to be linear if they are adjacent angles formed by two intersecting lines. The measure of a straight angle is ${{180}^{\circ }}$, so a linear pair of angles must add up to ${{180}^{\circ }}$.
Co-interior angles lie between two lines and on the same side of a transversal. In each diagram the two marked angles are called co-interior angles. If the two lines are parallel, then co-interior angles add to give ${{180}^{\circ }}$ and therefore, they are supplementary angles.