Question

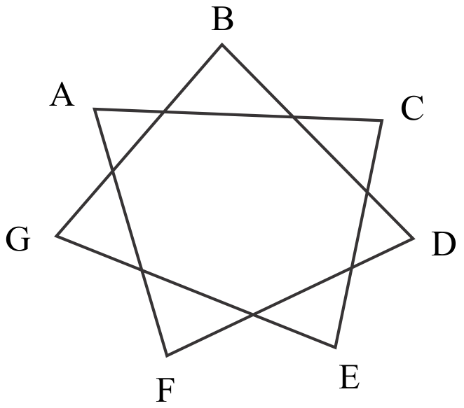
In the given figure, find the $\angle $($A+B+C+D+E+F+G$)=

Answer 1

Hint: If you observe the given figure it has 7 vertices. This figure is Heptagon. Heptagon is a polygon with 7 sides. To find all the required sum of angles, we apply the formula of the interior angles.

Complete step by step answer:
Sum of interior angles of an n sides polygon =$\left( {2n - 4} \right) \times 90$degrees…… $\left( 1 \right)$
Let us find the sum of interior angles of a heptagon.
So, the total number of sides in heptagon=7
Then n=7
From equation $\left( 1 \right)$,we have
Sum of interior angle of a heptagon=$\left( {2 \times 7 - 4} \right) \times 90$
$ \Rightarrow 10 \times 90 = 900$
One angle of a heptagon =$\dfrac{{900}}{7} = 128.57$degree
So, one angle of a triangle=$180 - 128.57 $
$= 51.43$ degrees
Another angle is $180-102.85$
$=77.14$degrees

Therefore, the sum of $\angle $(A+B+C+D+E+F+G)=$77.17 \times 7 = 540$degrees

Note:
Remember the formula of the sum of the interior angle of the “n” sides polygon. And the sum of all the angles of a triangle is 180 degrees. We need to be careful while observing the given figure to decide n value.