Question

In the given figure find the value of \[\angle x\] and \[\angle y\]

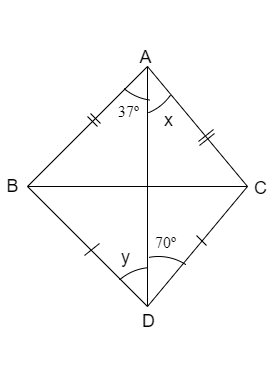
(a) \[x={{70}^{\circ }},y={{37}^{\circ }}\]
(b) \[x={{37}^{\circ }},y={{70}^{\circ }}\]
(c) \[x={{50}^{\circ }},y={{57}^{\circ }}\]
(d) \[x={{57}^{\circ }},y={{50}^{\circ }}\]

Answer 1

Hint: We solve this problem by using the properties of triangles.
We have the condition that sides represented with a single line are equal to each other and sides represented with a double line are equal to each other.
We have the condition of triangles that the angles opposite to equal sides are equal.
We use the congruence of triangles so that we can get the angles directly because the corresponding angles and sides of congruent triangles are equal.
By using the above condition we find the required values.

Complete step by step answer:
We are given the figure as

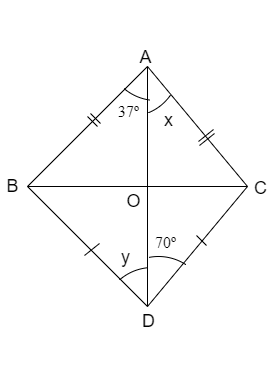
We know that the condition that sides represented with the single line are equal to each other and sides represented with the double line are equal to each other.
By using the above condition to the given figure we get
\[\Rightarrow BD=DC\]
\[\Rightarrow AB=AC\]
Let us consider that triangle \[\Delta ABC\]
We know that the condition that angles opposite to equal sides are equal
By using the above condition to \[\Delta ABC\] we get
\[\Rightarrow \angle ABC=\angle ACB=p\]
Let us consider that triangle \[\Delta DBC\]
We know that the condition that angles opposite to equal sides are equal
By using the above condition to \[\Delta DBC\] we get
\[\Rightarrow \angle DBC=\angle DCB=q\]
Now, let us consider the triangles \[\Delta AOB\] and \[\Delta AOC\]
Here, we have three conditions for triangles as
(1) \[AO=AO\left( \because \text{common side} \right)\]
(2) \[AB=AC\]
(3) \[\angle ABO=\angle ACO=p\]
By using the S.S.A congruency we can say that triangles \[\Delta AOB\] and \[\Delta AOC\] are congruent.
We know that the corresponding angles and sides of congruent triangles are equal.
By using the above condition we have
\[\begin{align}
  & \Rightarrow \angle BAO=\angle CAO \\
 & \Rightarrow x={{37}^{\circ }} \\
\end{align}\]
Now, let us consider the triangles \[\Delta DOB\] and \[\Delta DOC\]
Here, we have three conditions for triangles as
(1) \[DO=DO\left( \because \text{common side} \right)\]
(2) \[DB=DC\]
(3) \[\angle DBO=\angle DCO=q\]
By using the S.S.A congruency we can say that triangles \[\Delta DOB\] and \[\Delta DOC\] are congruent.
We know that the corresponding angles and sides of congruent triangles are equal.
By using the above condition we have
\[\begin{align}
  & \Rightarrow \angle BDO=\angle CDO \\
 & \Rightarrow y={{70}^{\circ }} \\
\end{align}\]
Therefore, we can conclude that the values of \[x,y\] are \[x={{37}^{\circ }},y={{70}^{\circ }}\]
So, option (b) is correct answer.

Note:
 Students may do mistake in taking the sides AD and CB
Here the lines AD and CB are not perpendicular because we do not know that type of quadrilateral.
There are some quadrilaterals whose diagonals are not perpendicular.
But students may consider that AD and BC are perpendicular that gives the wrong answer.