Question

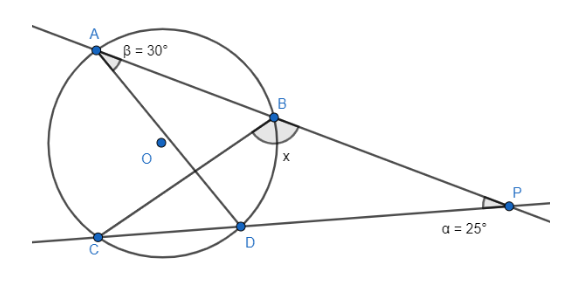
In the given figure, find the value of $x$?

Answer 1

Hint: We use the theorem of interior angles for a circle on an equal arc and they are equal. We also use the theorem that the sum of three angles of any triangle is always equal to \[{{180}^{\circ }}\]. We equate two interior angles of the triangle and find the required angle from the equation of $\angle BCP+\angle BPC+\angle CBP={{180}^{\circ }}$.

Complete step by step answer:
We use the theorem of interior angles for a circle on an equal arc of that circle. We know that if we take two interior angles which are on the same arc of a circle, then those angles will be equal. For our given circle of centre $O$, we take interior angles $\angle BAD$ and $\angle BCD$ which are on the same $\overset\frown{BD}$.

Therefore, \[\angle BAD=\angle BCD={{30}^{\circ }}\].
Also, we can tell \[\angle BCD=\angle BCP={{30}^{\circ }}\]
Now we take the $\Delta BCP$, whose three angles are $\angle BCP$, $\angle BPC$, $\angle CBP$.
The sum of three angles of any triangle is always equal to \[{{180}^{\circ }}\].
So, $\angle BCP+\angle BPC+\angle CBP={{180}^{\circ }}$. It is given that $\angle BPC={{25}^{\circ }},\angle CBP=x$.
Putting the values, we get ${{30}^{\circ }}+{{25}^{\circ }}+x={{180}^{\circ }}$.
Simplifying we get $x={{180}^{\circ }}-{{30}^{\circ }}-{{25}^{\circ }}={{125}^{\circ }}$.

Therefore, the value of $x$ is ${{125}^{\circ }}$.

Note: Similar theorem can be applied for the interior and centred angles where the exterior angles are half of the centred angles. Those angles have to be on the same arc. The direction of the angles is not important in this case.