Question

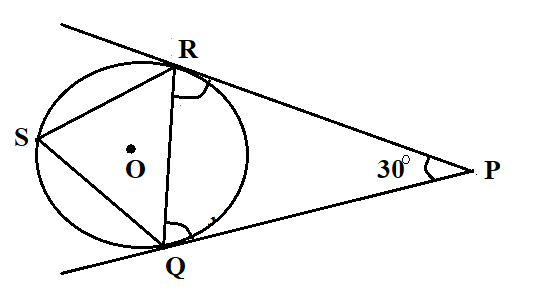
In the given figure, $SR\parallel QP$ and $\angle RPQ = {30^ \circ }$. Find the value of $\angle SQR$.

Answer 1

Hint: We use the theorem that tangents from the common point are equal and then calculate the values of $\angle PRQ$ and $\angle PQR$ by using angle sum property of a triangle. Then, we are given that $SR\parallel QP$, then apply the properties of parallel lines to find the angle $\angle SRQ$. Next, we will find $\angle RSQ$ by angles in the same segment theorem. At last, apply angle sum property to find the value of $\angle SQR$

Complete step-by-step answer:
We are given the value of $\angle RPQ = {30^ \circ }$ and $SR\parallel QP$
We have to find the value of $\angle SQR$
Here, we can see that tangents $PQ$ and $PR$ are drawn from a common point $P$, then
$PQ = PR$
It is known that angles opposite to equal sides are equal in a triangle $PQR$
Therefore, $\angle PRQ = \angle PQR$
And sum of all the angles of a triangle is ${180^ \circ }$
For triangle $PQR$, $\angle PRQ + \angle PQR + \angle RPQ = {180^ \circ }$
On substituting the value $\angle RPQ = {30^ \circ }$ and $\angle PRQ = \angle PQR$, we will get,
$
  \angle PQR + \angle PQR + {30^ \circ } = {180^ \circ } \\
   \Rightarrow 2\angle PQR = {150^ \circ } \\
   \Rightarrow \angle PQR = {75^ \circ } \\
$
Therefore, we have
$\angle PRQ = \angle PQR = {75^ \circ }$
Now, $SR\parallel QP$
Then, $\angle PQR = \angle SRQ = {75^ \circ }$ as they are alternate interior angles.
Also, the angle between the chord and tangent is equal to the angle in the alternate segment.
Therefore, $\angle PQR = \angle RSQ = {75^ \circ }$
Hence, in triangle, $RSQ$, we have
$\angle SRQ = \angle RSQ = {75^ \circ }$
Therefore, $RSQ$ is also an isosceles triangle.
And the sum of all the angles of a triangle is ${180^ \circ }$
$
  \angle SRQ + \angle RSQ + \angle SQR = {180^ \circ } \\
   \Rightarrow {75^ \circ } + {75^ \circ } + \angle SQR = {180^ \circ } \\
   \Rightarrow {150^ \circ } + \angle SQR = {180^ \circ } \\
   \Rightarrow \angle SQR = {30^ \circ } \\
$
Hence, the value of $\angle SQR$ is ${30^ \circ }$.

Note: Many students make mistakes by assuming that $RQ$ is perpendicular on $QP$ and $PR$. But, one has to take care $RQ$ is not the diameter as it is not passing from the centre. And the property states that the line from the centre is perpendicular to the tangent at the point of contact.