Question

In the given figure, TBP and TCQ are tangents to the circle whose center is O. Also, \[\angle PBA = {60^ \circ }\] and \[\angle ACQ = {70^ \circ }\]. Determine \[\angle BAC\] and \[\angle BTC\].

A. \[{50^ \circ },{60^ \circ }\]
B. \[{60^ \circ },{70^ \circ }\]
C. \[{50^ \circ },{70^ \circ }\]
D. \[{50^ \circ },{130^ \circ }\]

Answer 1

Hint: Here we join the radius of the circle OA, OB and OC. Use the concept of radius making the right angle at the point of contact with the tangent to find the angle and the using the property of isosceles triangle formed by radii of circle to find the angle contributing to \[\angle BAC\]. Using the property of the sum of opposite angles in a quadrilateral we find the value of \[\angle BTC\].
* The radius of the circle is perpendicular to the tangent at the point of contact.
* Isosceles triangle has two sides of equal length and the angles opposite to equal sides are equal in measure.
* In any quadrilateral, the sum of opposite sides is equal to \[{180^ \circ }\].

Complete step-by-step answer:
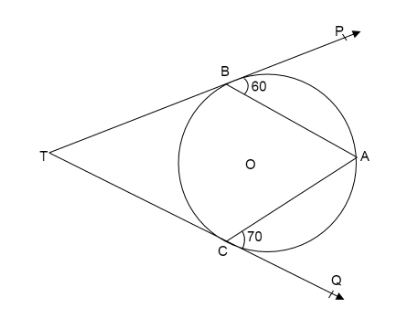
We are given the measure of angle\[\angle PBA = {60^ \circ }\]and\[\angle ACQ = {70^ \circ }\]
We join the radii of the circle with points A, B and C.

Use the property of tangents that the radius makes a right angle with the tangent at the point of contact.
Then, \[\angle OBP = {90^ \circ }\]
We can write \[\angle OBP = \angle OBA + \angle ABP\]
\[ \Rightarrow {90^ \circ } = \angle OBA + {60^ \circ }\]
Bring all constant values to one side of the equation
\[ \Rightarrow {90^ \circ } - {60^ \circ } = \angle OBA\]
\[ \Rightarrow {30^ \circ } = \angle OBA\]
Now we know that \[OA = OB\]as they both are radii of the same circle.
So, triangle OAB is an isosceles triangle
From the property of the isosceles triangle, the angles opposite to equal sides are equal.
\[ \Rightarrow \angle OBA = \angle OAB\]
Substitute the value of \[{30^ \circ } = \angle OBA\]
\[ \Rightarrow \angle OAB = {30^ \circ }\] … (1)
Also, \[\angle OCQ = {90^ \circ }\]
We can write \[\angle OCQ = \angle OCA + \angle ACQ\]
\[ \Rightarrow {90^ \circ } = \angle OCA + {70^ \circ }\]
Bring all constant values to one side of the equation
\[ \Rightarrow {90^ \circ } - {70^ \circ } = \angle OCA\]
\[ \Rightarrow {20^ \circ } = \angle OCA\]
Now we know that \[OA = OC\] as they both are radii of the same circle.
So, triangle OAC is an isosceles triangle
From the property of the isosceles triangle, the angles opposite to equal sides are equal.
\[ \Rightarrow \angle OCA = \angle OAC\]
Substitute the value of \[{20^ \circ } = \angle OCA\]
\[ \Rightarrow \angle OAC = {20^ \circ }\] … (2)
Now we know \[\angle BAC = \angle OAB + \angle OAC\]
Substitute the value from equations (1) and (2)
\[ \Rightarrow \angle BAC = {30^ \circ } + {20^ \circ }\]
\[ \Rightarrow \angle BAC = {50^ \circ }\]
Now we have a quadrilateral ABTC. Then sum of opposite angles is \[{180^ \circ }\]
We have opposite angles \[\angle BTC\]and\[\angle BAC\]
\[ \Rightarrow \angle BTC + \angle BAC = {180^ \circ }\]
Substitute the value of\[\angle BAC = {50^ \circ }\]
\[ \Rightarrow \angle BTC + {50^ \circ } = {180^ \circ }\]
Shift all the constant values to one side of the equation
\[ \Rightarrow \angle BTC = {180^ \circ } - {50^ \circ }\]
\[ \Rightarrow \angle BTC = {130^ \circ }\]
So, the angles \[\angle BAC,\angle BTC\] are \[{50^ \circ },{130^ \circ }\]

So, option D is correct.

Note: Students many times get confused with angles given in the diagram i.e. \[\angle PBA = {60^ \circ }\] and \[\angle ACQ = {70^ \circ }\] as the angles made by radius with the tangents. Keep in mind radius is always perpendicular to the tangent at point of contact. Always change the sign from negative to positive and vice versa when shifting the values from one side to another.