Question

In the given figure the wedge is fixed, pulley is light and frictionless and string is light Surface AB is frictionless whereas AC is rough If the block of mass \[3\;{\rm{m}}\] slides down with constant velocity, then the coefficient of friction between surface AC and the block is

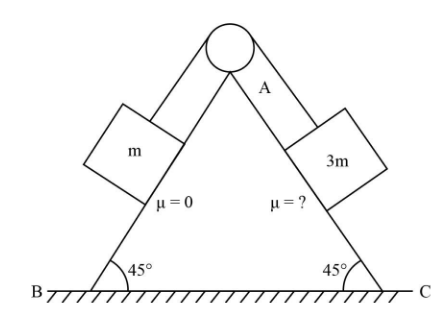
A. $\dfrac{1}{3}$
B. $\dfrac{2}{3}$
C. $\dfrac{1}{2}$
D. $\dfrac{4}{3}$

Answer 1

Hint:This question is based on the concept of mass and pulley. There are two blocks available connected by the pulley. One block of mass \[3\;{\rm{m}}\]slides down and tension is acting on the string connecting the two blocks. On another block that has mass m moving with constant velocity and tension $T$ is acting on the string and also $mg\sin \theta $ acting on the block. We have to equate the equations and find the coefficient of friction.

Complete step by step answer:
We know that if the block is moving with constant velocity then the acceleration becomes zero. First, we consider the mass $m$. On this block of $m$, there are several forces act on the block, one is tension force and another force is $mg\sin \theta $.

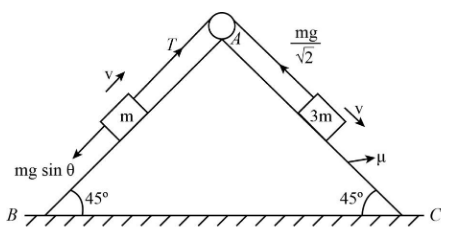
Now, we can equate the two forces we get,
$T = mg\sin \theta $
Here, $\theta $ is $45^\circ $.
Substitute the values in the above equation we get,
$
T = mg\sin 45^\circ \\
\Rightarrow T = \dfrac{{mg}}{{\sqrt 2 }}
$
Now, on the second block, the tension is the same. So, we can calculate the coefficient of friction of block \[3\;{\rm{m}}\].

Now , the expression of coefficient of friction is given as,
$f = \mu N$
Here, $\mu $ is the coefficient of friction and $N$ is the normal force.
Substitute the values in the above equation we get,
\[
3mg\sin 45^\circ = \dfrac{{mg}}{{\sqrt 2 }} + 3mg\cos 45^\circ \\
\Rightarrow 2 = 3\mu \\
\therefore\mu = \dfrac{2}{3}
\]
Therefore, the coefficient of friction is $\dfrac{2}{3}$.

Thus, the correct option is B.

Note:In this question, the students must know how to resolve forces and must have knowledge of the term frictional force and tension force. On the block of mass $3\;{\rm{m}}$ the frictional force is $3mg\sin 45^\circ $ because two components are formed one is normal $3mg\cos 45^\circ $ and another is frictional force $3mg\sin 45^\circ $. And the tension force also acts on the string. Since the pulley is frictionless, the tension remains the same on both sides.