Question

In the given figure triangle ABC is right angled at B. ACDE and BCGF are squares. Then prove that
\[\begin{align}
  & a)\Delta BCD\cong \Delta GCA \\
 & b)AG=BD \\
\end{align}\]

Answer 1

Hint: Now we know that sides of the square are equal. Hence using this property we will get AC = CD and BD = GC. Now we will prove $\angle ACG=\angle BCD$ with the help of property of square which says each angle of square is ${{90}^{\circ }}$. Now we can use the SAS test to prove congruency and then by CPCT, we can also prove BD = AG.

Complete step-by-step answer:
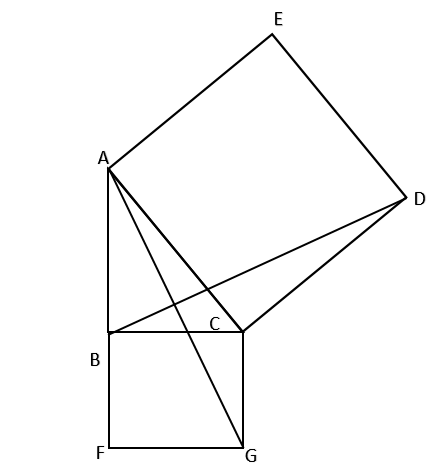
Now first let us consider the square ABCD.
Now we know that the sides of squares are congruent. Hence we get
AC = CD……………….. (1)
Now we also know that each angle of the square is equal to ${{90}^{\circ }}$ . Hence we also have
$\angle ACD={{90}^{\circ }}$……………….. (2)
Now consider square BCGF.
Now again using the property of square that the sides of square are equal we get
BC = CG …………………. (3)
And also each angle of the square is equal to ${{90}^{\circ }}$ . Hence we get
$\angle BCG={{90}^{\circ }}$ …………………… (4)
Now first let us consider $\angle BCD$
Now from figure we can say that $\angle BCD=\angle BCA+\angle ACD$
Now substituting the value from equation (2) we get
$\angle BCD=\angle BCA+{{90}^{\circ }}$…………………………… (5)
In a similar way let us consider $\angle ACG$ . With the help of figure we can say that
$\angle ACG=\angle GCB+\angle BCA$
Now substituting value from equation (4)
$\angle ACG={{90}^{\circ }}+\angle BCA$………………………….. (6)
From equation (5) and equation (6) we get.
$\angle ACG=\angle BCD$ …………………………… (7)
Now consider two triangle BCD and triangle ACG.
Now in this triangle we have
AC = CD {from equation (1)}
BC = CG {from equation (3)}
$\angle ACG=\angle BCD$ {From equation (7)}
Now from the SAS test of congruence we can say that \[\Delta BCD\cong \Delta GCA\].
Now we know that congruent parts of congruent triangles are equal.
Hence we get BD = AG.

Note: Note that while writing congruent triangles we write corresponding sides properly. For example if AB = QR in a triangle and we write $\Delta ABC\cong \Delta PQR$ then it's wrong since the corresponding side to AB is PQ and not QR.