Question

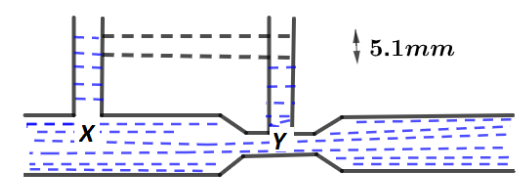
In the venturimeter as shown, water is flowing. Speed at $x$ is $2\,cm\,{\sec ^{ - 1}}$. The Speed of water at $y$ is ? $(g = 1000\,cm\,{\sec ^{ - 2}})$
A. $23\,cm\,{\sec ^{ - 1}}$
B. $32\,cm\,{\sec ^{ - 1}}$
C. $101\,cm\,{\sec ^{ - 1}}$
D. $1024\,cm\,{\sec ^{ - 1}}$

Answer 1

Hint: In order to solve this question, we will use the definition of venturimeter. Venturimeter is a device that is used to measure the rate of flow of liquid through a pipe. This device is based on the principle of Bernoulli’s equation. It has three parts: Covering part, throat and Diverging part. Bernoulli’s principle depicts that when velocity increases pressure decreases. Water flows as there is pressure difference between inlet pipe and throat which can be measured using a differential manometer. After getting pressure difference flow rate is calculated

Complete step by step answer:
Given in question ${v_1} = 2\,cm\,{\sec ^{ - 1}}$ where ${v_1}$ is velocity of fluid at $x$
Similarly ${v_2} = v\,cm\,{\sec ^{ - 1}}$ , where ${v_2}$ is velocity of fluid at $y$
And $h = 5.1\,mm = 0.51\,cm$
Using Bernoulli’s Principle at $x$ and $y$ we get
$\dfrac{{{p_1}}}{{\rho g}} + \dfrac{{{v_1}^2}}{{2g}} + {z_1} = \dfrac{{{p_2}}}{{\rho g}} + \dfrac{{{v_2}^2}}{{2g}} + {z_2}$
$ \Rightarrow \dfrac{{{p_1}}}{{\rho g}} + \dfrac{{{v_1}^2}}{{2g}} = \dfrac{{{p_2}}}{{\rho g}} + \dfrac{{{v_2}^2}}{{2g}}$ since $({z_1} = {z_2} = 0)$ As the tube is horizontal
$ \Rightarrow \dfrac{{{p_1} - {p_2}}}{{\rho g}} = \dfrac{{{v_2}^2 - {v_1}^2}}{{2g}}$
$ \Rightarrow h = \dfrac{{{v_2}^2 - {v_1}^2}}{{2g}}$ Where $(h = \dfrac{{{p_1} - {p_2}}}{{\rho g}})$ is the height difference between two water level at x & y
${v_2}^2 = {v_1}^2 + 2gh$
Putting values in above equation we get
${v^2} = {(2cm{\sec ^{ - 1}})^2} + (2 \times 1000\,cm\,{\sec ^{ - 2}} \times 0.51\,cm)$
$ \Rightarrow {v^2} = 1024\,c{m^2}\,{\sec ^{ - 2}}$
$ \Rightarrow v = 32\,cm\,{\sec ^{ - 1}}$

Hence,The Speed of water at $y$ is $32\,cm\,{\sec ^{ - 1}}$.

Note: It should be remembered that, continuity equation always valid at both $x$ and $y$ so flow would be continuous also in Bernoulli’s Principle we have put ${z_1}\& {z_2}$ equal to zero because the venturimeter is horizontal in nature. It can be viewed that velocity at $y$ is greater than velocity at $x$ even pressure at $y$ is less than pressure at $x$ this clearly depicts the proof that Bernoulli's flow in the venturi meter could be laminar flow because of fluid continuity.