
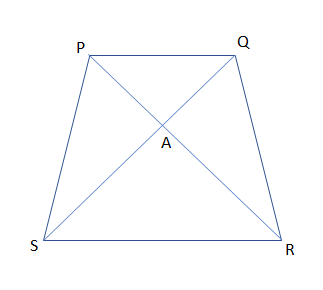
In trapezium PQRS, side PQ is parallel to side SR and AR=5AP and also AS=5AQ, then prove that SR=5PQ.

Answer
493.5k+ views
1 likes
Hint: First, we know from the study of parallel lines that in between two parallel lines if any transverse line cuts both the lines then the angles made by that lines are always equal. Then, by using the same concept to the given lines which are parallel PQ and RS, so in
Complete step by step answer:
In this question, we are supposed to prove that SR=5PQ, when PQRS is a trapezium with side PQ, is parallel to side SR and AR=5AP and also AS=5AQ.
So, before proceeding for this, we must understand the figure that side PQ is parallel with side SR and other conditions in a trapezium PQRS with center A as:
Now, we know from the study of parallel lines that in between two parallel lines if any transverse line cuts both the lines then the angles made by that lines are always equal.
So, by using the same concept to the given lines which are parallel PQ and RS, so in
So, by using the AAA property of congruency, we get
So, by using the above concept, we get:
Now, we are given in the question the condition that AR=5AP and by substituting this value in the above expression, we get:
So, we get the condition that SR=5PQ.
Hence, the given condition is proved.
Note:
Now, to solve these types of questions we need to know some of the basics of the concept of parallel lines intersected by a traverse line as in the above question the diagonal are intersecting the parallel sides PQ and RS. So, we get all the interior angles as equal in between parallel lines when it is intersected by a straight transverse line.
Complete step by step answer:
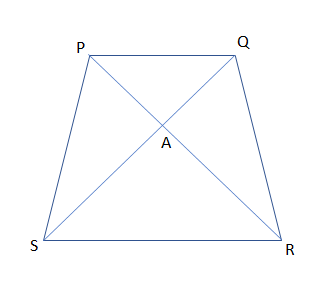
In this question, we are supposed to prove that SR=5PQ, when PQRS is a trapezium with side PQ, is parallel to side SR and AR=5AP and also AS=5AQ.
So, before proceeding for this, we must understand the figure that side PQ is parallel with side SR and other conditions in a trapezium PQRS with center A as:

Now, we know from the study of parallel lines that in between two parallel lines if any transverse line cuts both the lines then the angles made by that lines are always equal.
So, by using the same concept to the given lines which are parallel PQ and RS, so in
So, by using the AAA property of congruency, we get
So, by using the above concept, we get:
Now, we are given in the question the condition that AR=5AP and by substituting this value in the above expression, we get:
So, we get the condition that SR=5PQ.
Hence, the given condition is proved.
Note:
Now, to solve these types of questions we need to know some of the basics of the concept of parallel lines intersected by a traverse line as in the above question the diagonal are intersecting the parallel sides PQ and RS. So, we get all the interior angles as equal in between parallel lines when it is intersected by a straight transverse line.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




