Question

In triangle ABC, if \[AB = AC\] and \[\angle B = 50^\circ \], then angle A is equal to
(a) \[40^\circ \]
(b) \[50^\circ \]
(c) \[80{}^\circ \]
(d) \[130^\circ \]

Answer 1

Hint: Here, we need to find the measure of angle A. As the two sides are equal, so we can say that the given triangle is an isosceles triangle. We will use the property of an isosceles triangle, and then the angle sum property of a triangle to find the required measure of angle A.

Complete step-by-step answer:
First, we will draw the given isosceles triangle.

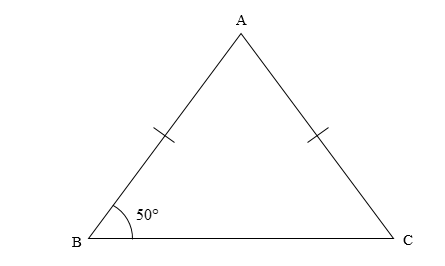
The isosceles triangle property states that the angles opposite to equal sides are also equal.
It is given that in the isosceles triangle ABC, \[AB = AC\].
Therefore, we get
\[\angle B = \angle C\]
Substituting \[\angle B = 50^\circ \] in the equation, we get
\[\angle C = 50^\circ \]
Now, we will use the angle sum property of a triangle.
The angle sum property of a triangle states that the sum of the measures of the three interior angles of a triangle is always \[180^\circ \].
Therefore, in triangle ABC, we get
\[\angle A+\angle B+\angle C=180{}^\circ \]
Substituting \[\angle B = 50^\circ \] and \[\angle C = 50^\circ \] in the equation, we get
\[ \Rightarrow \angle A + 50^\circ + 50^\circ = 180^\circ \]
This is a linear equation in terms of \[\angle A\]. We will solve this equation to find the measure of angle A.
Adding the like terms in the expression, we get
\[ \Rightarrow \angle A + 100^\circ = 180^\circ \]
Subtracting \[100^\circ \] from both sides of the equation, we get
\[ \Rightarrow \angle A + 100^\circ - 100^\circ = 180^\circ - 100^\circ \]
Thus, we get
\[ \Rightarrow \angle A = 80^\circ \]
\[\therefore \] We get the measure of angle A as \[80^\circ \].
Thus, the correct option is option (c).

Note: We know that a triangle is a two-dimensional geometric shape and has 3 sides. There are different types of triangles based on sides and angles. When two sides of a triangle are equal then the triangle is called an isosceles triangle. If all three sides are equal, then the triangle is called an equilateral triangle. When one of the angles of a triangle is equal to \[90^\circ \] then the triangle is called a right-angled triangle. Now using these definitions we can easily find the type of the triangle and apply its property.