Question

In $$\triangle OPQ$$, right angled at P, OP = 7 cm, OQ - PQ= 1 cm. Determine the values of $$\sin Q$$ and $$\cos Q$$.

Answer 1

Hint: In this question it is given that $\triangle OPQ$ is a right angle triangle, right angled at P, OP = 7 cm, OQ - PQ= 1 cm. We have to determine the values of $$\sin Q$$ and $$\cos Q$$. So to understand it in better we have to draw the diagram,

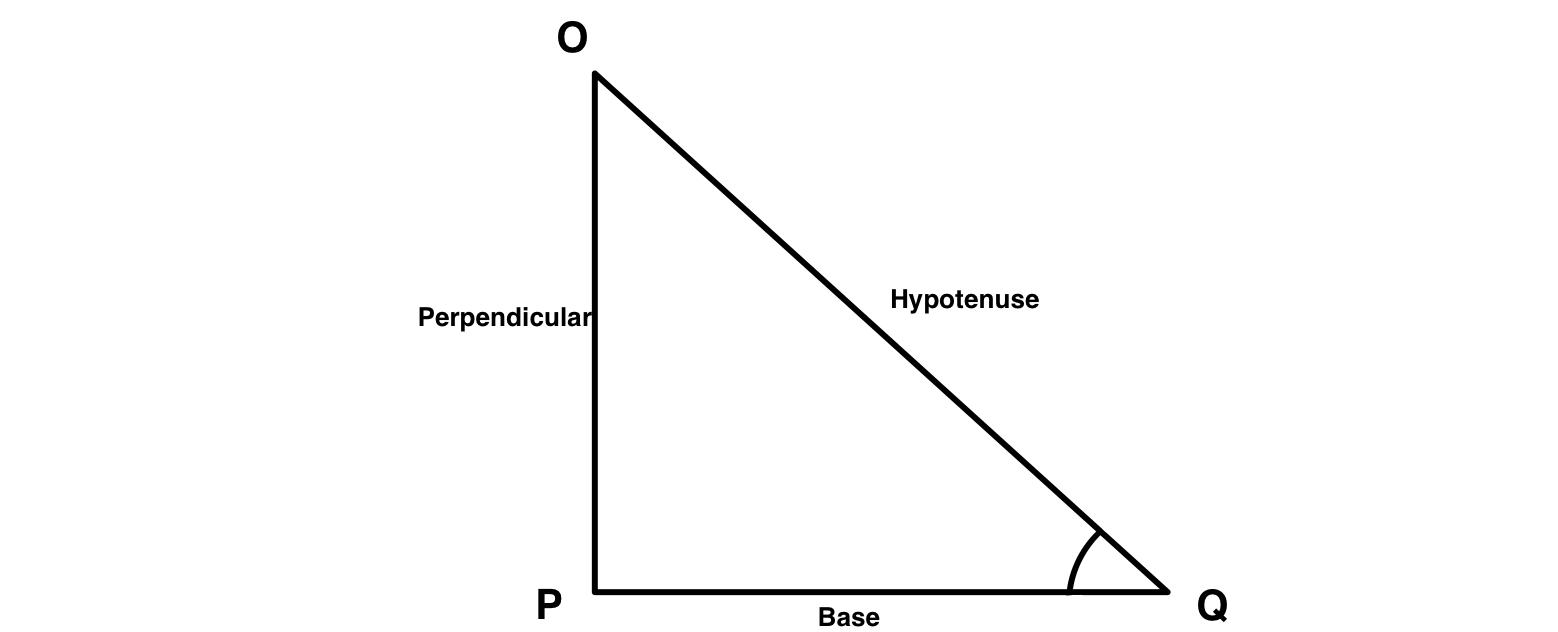
So to find the solution we need to know the Pythagorean theorem which states that for an right angle triangle the square of the hypotenuse is equal to the summation of the sqof base and perpendicular(height).
i.e, $$\left( \text{Hypotenuse} \right)^{2} =\left( \text{Perpendicular} \right)^{2} +\left( \text{Base} \right)^{2} $$.......(1)

Complete step-by-step answer:
Let us consider the length of PQ to be x cm.
Here it is given that OP = 7 cm and OQ - PQ =1
Therefore, OQ = 1+PQ = (1+x) cm.
Now by Pythagorean theorem we can write,
$$\left( \text{Hypotenuse} \right)^{2} =\left( \text{Perpendicular} \right)^{2} +\left( \text{Base} \right)^{2} $$
$$\Rightarrow \left( OQ\right)^{2} =\left( OP\right)^{2} +\left( PQ\right)^{2} $$
$$\Rightarrow \left( 1+x\right)^{2} =7^{2}+x^{2}$$.........(2)
Now as we know that $$\left( a+b\right)^{2} =a^{2}+2ab+b^{2}$$.
So by using this identity $$\left( 1+x\right)^{2} $$ can be written as,
$$\left( 1+x\right)^{2} =1^{2}+2\times 1\times x+x^{2}$$
                $$=1+2x+x^{2}$$
Therefore the equation (2) can be written as,
$$1+2x+x^{2}=7^{2}+x^{2}$$
$$\Rightarrow 1+2x+x^{2}=49+x^{2}$$
$$\Rightarrow 1+2x=49+x^{2}-x^{2}$$ [by changing the side of $$x^{2}$$]
$$\Rightarrow 1+2x=49$$
$$\Rightarrow 2x=49-1$$
$$\Rightarrow 2x=48$$
$$\Rightarrow x=\dfrac{48}{2}$$
$$\Rightarrow x=24$$
Therefore the length of the base PQ = 24 cm and the length of the hypotenuse OQ = 1+x = (1+24) cm = 25 cm.
Now we have to find the given trigonometric ratios,
As we know that $$\sin Q=\dfrac{\text{Perpendicular} }{\text{Hypotenuse} }$$
Therefore, from the diagram we can write,
$$\sin Q=\dfrac{OP}{OQ}$$
    $$=\dfrac{7}{25}$$
Also we know that the trigonometric ratio $$\cos Q$$ can be written as,
$$\cos Q=\dfrac{\text{Base} }{\text{Hypotenuse} }$$
    $$=\dfrac{PQ}{OQ}$$
    $$=\dfrac{24}{25}$$
Therefore we get,
$$\sin Q=\dfrac{7}{25\ } \text{and} \ \cos Q=\dfrac{24}{25}$$

Note: To solve this type of question you need to know that In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. The most widely used trigonometric functions are the sine, the cosine, and the tangent which can be written as $$\sin \theta ,\ \cos \theta ,\ \tan \theta$$, where $$\theta$$ is the acute angle of an right angle triangle.