Question

In two concentric circles, chord AB of the outer circles cuts the inner circle at C and D. Prove that AC=BD.

Answer 1

Hint: In order to prove this question we will first draw a perpendicular on a line and proceed further by using the property of the circle as the perpendicular drawn from the center of a circle to a chord bisects the chord of the circle.

Complete step-by-step answer:

Let a line intersects two concentric circles with center O at A, B, C and D .

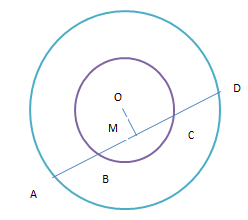
To Prove:
AB= CD

Construction – Draw OM perpendicular from O on a line.

Proof:

We know that the perpendicular drawn from the center of a circle to the chord bisects the chord.

Here, AD is a chord of a larger circle.
${\text{OM}} \bot {\text{AD}}$ is drawn from O.
OM bisects AD as ${\text{OM}} \bot {\text{AD}}$
${\text{AM}} = {\text{ MD}}.........{\text{(1)}}$

Here, BC is the chord of the smaller circle.
OM bisects BC as ${\text{OM}} \bot {\text{ BC}}$ .
${\text{BM}} = {\text{MC}}..........{\text{(2)}}$

From (1) and (2),

On subtracting equation (1) and from (2)
$
  {\text{AM - BM}} = {\text{MD - MC}} \\
  {\text{AB}} = {\text{CD}} \\
 $

Hence, ${\text{AB}} = {\text{CD}}$

Note: In order to solve this question, we use the property of the circles. So remember all the properties of the circles. Also remember when a line bisects the other line perpendicularly; it divides the line into two equal parts. Also be familiar with the terms like chord, secant, tangent. A secant is simply a line that intersects two points of the circle.