Question

In which figure does the shaded part represent 0.3?
A.

B.

C.

D.

Answer 1

Hint: We use the concept of fraction and first convert the given decimal number in fraction form. The denominator represents the total number of parts in which the figure is divided and the numerator represents the number of shaded parts of the figure. We check for each figure if the fraction formed equals the fraction for decimal number.
Convert a decimal number into fraction by writing the number in numerator (without decimal point) and writing \[{10^n}\] in a denominator where \[n\]is the number of places where the decimal is placed (counting from right end).

Complete step by step answer:
We are given the decimal number 0.3
We first convert the decimal number into fraction
Since the number of digits after the decimal place in the number 0.3 is 1, we write\[{10^1} = 10\] in the denominator and 3 in the numerator
\[ \Rightarrow 0.3 = \dfrac{3}{{10}}\] … (1)
Now we form a fraction for each figure where the numerator contains a number of shaded parts and the denominator contains a total number of parts.
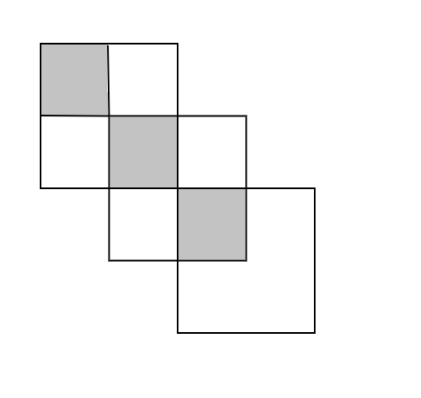
A.

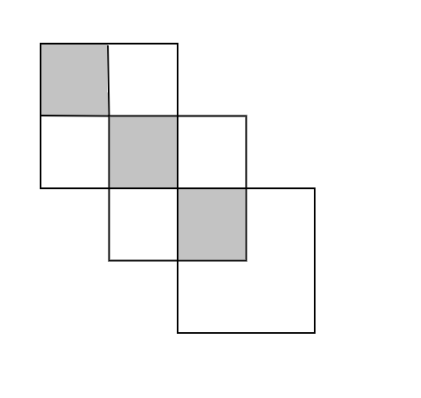
Here we have a total number of parts in which the figure is divided as 8 but the figure is not completely divided into equal parts. The number of shaded parts of the figure is 3.
We cannot form a fraction here as the figure is not divided into equal parts.
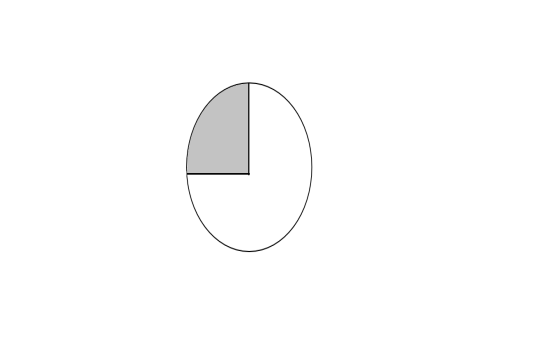
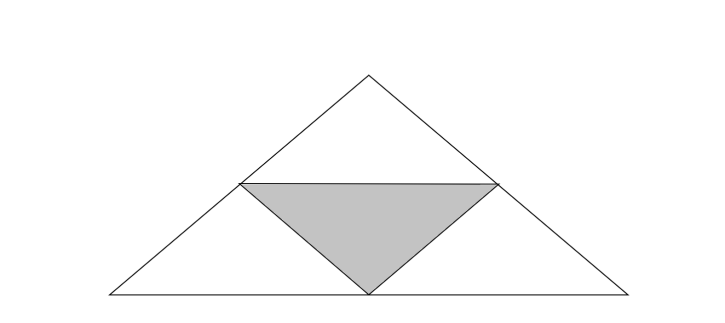
B.

Here we have a total number of parts in which the figure is divided as 2 but the figure is not completely divided into equal parts. The number of shaded parts of the figure is 1.
We cannot form a fraction here as the figure is not divided into equal parts.
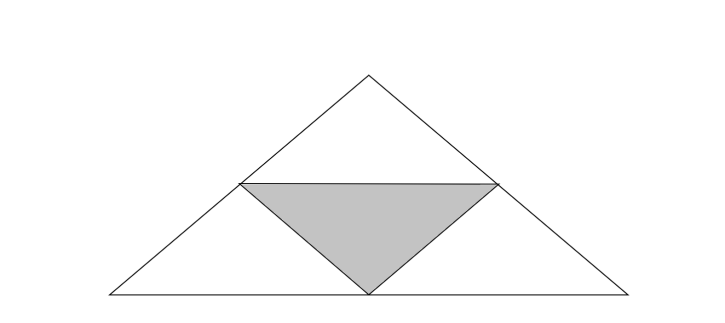
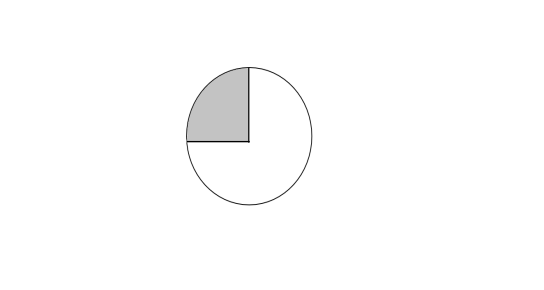
C.

Here we have a total number of equal parts in which the figure is divided as 4. The number of shaded parts of the figure is 1.
We can form a fraction here as the figure is divided into equal parts.
Fraction is \[\dfrac{1}{4}\]
Converting the fraction into decimal we get \[\dfrac{1}{4} = 0.25\]
Since 0.25 is not equal to 0.3, the figure doesn’t represent 0.3
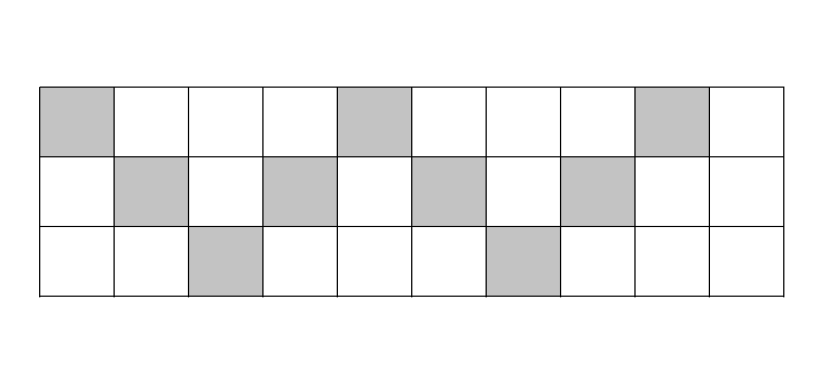
D.

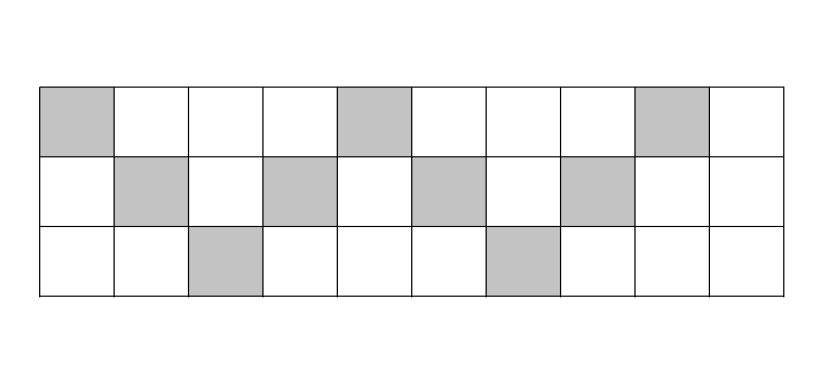
Here we have a total number of equal parts in which the figure is divided as 30. The number of shaded parts of the figure is 9.
We can form a fraction here as the figure is divided into equal parts.
Fraction is \[\dfrac{9}{{30}}\]
Cancel same factors from numerator and denominator of the fraction
Fraction is \[\dfrac{3}{{10}}\]
Converting the fraction into decimal we get \[\dfrac{3}{{10}} = 0.3\]
Since the fraction form of the figure is equal to 0.3, we can say the figure represents the decimal number 0.3.

\[\therefore \]Option D is correct.

Note: Many students make mistake of forming fractions in first and second part which is wrong as those two figures do not have all parts equal, keep in mind fraction means the part of the whole but we need to divide the figure into equal parts then we can form a fraction in terms of parts.