Question

In which of the following closed figure diagonals bisect each other at \[{90^ \circ }\].
(A) Rhombus
(B) Quadrilateral
(C) Circle
(D) Trapezium

Answer 1

Hint: Diagonals are the line segments that join the opposite vertices of the quadrilaterals. To find the diagonals of which closed figure bisect each other at right angle, first draw both diagonals and then by congruence and similarity of triangles we get the relation between the angles and then with the help of straight angle on line segment we can find the angle between the diagonals.

Complete step-by-step solution:
Option (A) is Rhombus firstly drawing its diagonals; we get the below drawn figure.

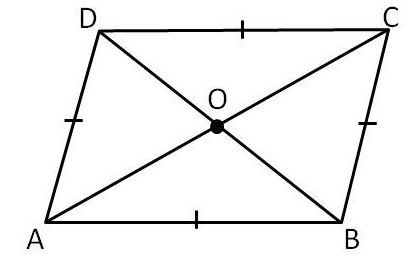
Here, $ABCD$ is a rhombus and “$AC$” and “$BD$” are its two diagonals.
We have to check either the diagonals $AC$ and $BD$ bisect each other at right angles. That is \[\angle AOB\], $\angle BOC$,$\angle COD$ and $\angle AOD$ are right angles or not.
 Now, we take two triangles $\Delta AOB$ and $\Delta BOC$
Since all the sides of rhombus of rhombus are equal,
So, side $AB = $ Side $BC$-----------(1)
Half of the diagonal $BD$ that is $OB$ is common to both the triangles.
$OB = OB$-------------(2)
We know that the diagonal of rhombus bisect the vertices through which it passes,
So, $\angle ABO = \angle CBO$-----------(3)
So, by combining (1), (2) and (3) we can say that triangle $\Delta AOB$ is congruent to the triangle $\Delta {\rm B}OC$ by side angle side ( $SAS$ ) congruence theorem.
i.e $\Delta AOB \cong \Delta BOC$.
By congruent part of congruence theorem (CPCT),
$\angle AOB = \angle BOC$
Now, $AC$ is a line segment. So,
$\angle AOB + \angle BOC = 18{0^ \circ }$ (straight angle)
$\angle AOB = BOC$,
 $
  2\angle AOB = 18{0^ \circ } \\
   \Rightarrow \angle {\rm A}{\rm O}{\rm B} = \dfrac{{{{180}^ \circ }}}{2} \\
  \therefore \angle AOB = {90^ \circ }
 $
So, $\angle BOC = {90^ \circ }$
Similarly, $\angle COD$ and $\angle AOD$are right angle.
Thus, both the diagonals of rhombus bisect each other at right angles.
Similarly, we can check in case any quadrilateral like rectangle, parallelogram, Square, trapezium, kite but we get only in case of rhombus and square, the diagonals bisect each other at right angles.
Thus, option (B) and (D) are incorrect.
Now, Option (C) In circle there are no particularly defined diagonals, so here the bisection of diagonals is not possible.

Hence, option (A) is correct.

Note: Similarly, we can prove that the diagonals of a square bisect each other at right angles.
By the congruence theorem we can also prove that opposite angles of the rhombus and parallelogram are equal. For this we take the opposite triangle that is $\Delta AOB$ and $\Delta COD$, then proceed as above.