Question

Into a cylindrical drum of radius 4.9m and height 3.6m. how many bags of grain can be emptied if the space required for each bag is \[1.8{m^3}\].( take \[\pi = 3.14\])

Answer 1

Hint:This problem is related to the area and volume concept. Here you have to carefully observe that when we empty the grain bags into the cylindrical drum that it will occupy the volume of the drum. So we will find the volume of the cylindrical drum and then divide it with the volume of one bag of grain that is space occupied by one bag. So that we can get the number of bags that can be emptied in it.

Formula used:
Volume of the cylinder is given by \[\pi {r^2}h\].
Where,$r$ is the radius of the cylinder and $h$ is the height of the cylinder

Complete step by step answer:
Given is the cylindrical drum. The radius of the drum is 4.9m and height is 3.6m.

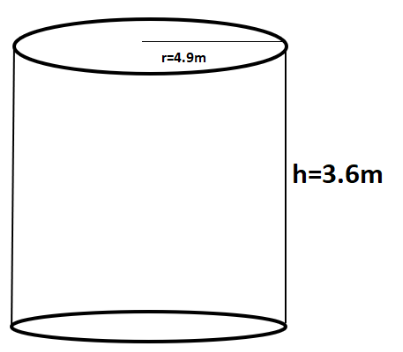
Using this data we will find the volume of the drum first.
Using the formula we will get,
\[{V_{cylindrical{\text{ }}drum}} = \pi {r^2}h\]
Putting the values we get,
\[{V_{cylindrical{\text{ }}drum}} = 3.14 \times {\left( {4.9} \right)^2} \times 3.6\]
On taking the product,
\[{V_{cylindrical{\text{ }}drum}} = 271.40\]
This is equivalent to,
\[{V_{cylindrical{\text{ }}drum}} \simeq 271\]

Now this is the total volume of the drum. Now in order to find how many bags can be emptied we will divide the volume of the cylinder by the space occupied by one bag.
Number of bags that can be emptied \[ = \dfrac{{{V_{cylindrical{\text{ }}drum}}}}{{space{\text{ }}occupied{\text{ }}by{\text{ }}one{\text{ }}bag}}\]
Putting the values we get,
\[\dfrac{{271}}{{1.8}}\]
On dividing we get,
\[150.55\]

So around 150 bags can be emptied in that drum.

Note:There is no need for an area. It is the same as we do every year at our home related to our grains. We also assume the volume of one bag of grain and the vessel or storage tank we are going to store in it. So this is totally dependent on the concept of volume. Now the answer is rounded off because we have to answer the exact number of bags if in the options we are available with the decimal choices we can tick the correct or that which we have obtained.