Question

In\[\vartriangle ABC\] points \[P{\text{ }} and {\text{ }}Q\] trisect side \[AB\] points \[T{\text{ }} and {\text{ }}U\] trisect \[AC\] and points \[R{\text{ }} and {\text{ }}S\] trisect\[BC\]. Then the perimeter of hexagon\[PQRSTU\] is how many times the perimeter of\[\vartriangle ABC\]?
A \[\dfrac{1}{3}\]
B\[\dfrac{2}{3}\]
C \[\dfrac{1}{6}\]
D \[\dfrac{1}{2}\]

Answer 1

Hint: In this question we are given a \[\vartriangle ABC\] in which the points \[P{\text{ }} and {\text{ }}Q\] trisect side\[AB\] points \[T{\text{ }} and {\text{ }}U\] trisect\[AC\] and points \[R{\text{ }} and {\text{ }}S\] trisect\[BC\] and we are asked here that the perimeter of hexagon PQRSTU is how many times the perimeter of \[\vartriangle ABC\]. For this we need to visualize the given condition by a diagram then using the trisecting condition given the question for the solving for the perimeter of the resultant hexagon \[PQRSTU\] and then finding the correct answer.

Complete step-by-step answer:
Here we are given a triangle \[\vartriangle ABC\] in which the points \[P{\text{ }} and {\text{ }}Q\] trisect side\[AB\] points \[T{\text{ }} and {\text{ }}U\] trisect \[AC\] and points \[R{\text{ }} and {\text{ }}S\] trisect\[BC\]. Here we are asked that the perimeter of hexagon PQRSTU is how many times the perimeter of \[\vartriangle ABC\]. For this we need to first find the perimeter of the resultant hexagon formed by the joining the points that trisect the sides of the \[\vartriangle ABC\] that is \[PQRSTU\]
For this we need to visualize the whole condition of the question by a diagram that is –

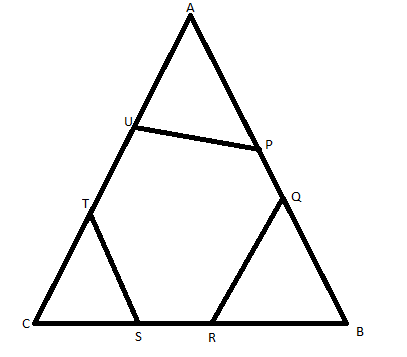
Here now let us assume that in \[\vartriangle ABC\]
\[
  AB = x \\
  BC = y \\
  CA = z \\
\]
As a point trisecting any line divides into three equal parts
Now as points \[P{\text{ }} and {\text{ }}Q\] trisects the side \[AB\] so the \[AQ = QP = BP = \dfrac{x}{3}\]
(As we have assumed \[AB = x\])
Similarly the points \[R{\text{ }} and {\text{ }}S\] trisects the side \[BC\] so the \[BR = RS = SC = \dfrac{y}{3}\]
(As we have assumed \[BC = y\])
similarly the points \[T{\text{ }} and {\text{ }}U\] trisects the side \[AC\] so the \[AT = TU = UC = \dfrac{z}{3}\]
(As we have assumed \[AC = z\])
Now the perimeter of the hexagon \[PQRSTU = PQ + QT + TU + US + RS + PR\]
As the perimeter is equal to the sum of all the sides
Also the opposite sides of the hexagon are equal it is a standard property of the hexagon
So the perimeter of the hexagon becomes –
\[PQRSTU = (\dfrac{x}{3} + \dfrac{y}{3} + \dfrac{z}{3}){\times}2\]
As the \[
  PQ = \dfrac{x}{3} \\
  RS = \dfrac{y}{3} \\
  TU = \dfrac{z}{3} \\
\](from the above simplification of the given conditions)
Now we have to find that the perimeter of hexagon \[PQRSTU\] is how many times the perimeter of \[\vartriangle ABC\]. For which we have to find the perimeter of the triangle \[\vartriangle ABC\] that is as perimeter is equal to the sum of all the sides then the perimeter is-
\[AB + BC + AC = x + y + z\]
Now to find the perimeter of the hexagon \[PQRSTU\] is how many times the perimeter of \[\vartriangle ABC\].
We need to find the fraction that is-
\[\dfrac{{{\text{ }} perimeter {\text{ }}of{\text{ }}the{\text{ }}hexagon PQRSTU}}{{{\text{ }}perimeter{\text{ }} of {\text{ }}the{\text{ }} triangle\vartriangle ABC}}\]
Putting the values the fraction becomes-
\[\dfrac{{(\dfrac{x}{3} + \dfrac{y}{3} + \dfrac{z}{3}){\times}2}}{{x + y + z}}\]
On further simplification the answer comes out is-
 \[ = \dfrac{2}{3}\]
So perimeter of hexagon \[PQRSTU\] is \[ = \dfrac{2}{3}\] times the perimeter of \[\vartriangle ABC\]
Which is similar to the option B in the question that is B \[\dfrac{2}{3}\]
Hence the correct answer is the option B .

Note: While solving such kind of questions drawing a diagram and visualizing the given conditions is the main key to the solution and one should also know how to use the basic properties related to any shape may it be circle, rectangle, square and much more in this it was hexagon.