Question

What is the inverse of a logarithmic function?

Answer 1

Hint: For solving this question you should know about the inverse of logarithmic functions. The inverse of the logarithmic functions calculated by converting the function in base e from each side then convert it to an exponential equation with base e, then make it as a isolated term and then check the domain of the function and then you can check your answer by the symmetricity of line \[y=x\].

Complete step-by-step solution:
According to our question it is asked to us to find the inverse of a logarithmic function.
The inverse of a logarithmic function is an exponential function. And if we notice them the graphs of logarithmic function and inverse logarithmic function is equal to the mirror image of each other with respect to the line \[y=x\].
If you made the graph on a paper and if you fold this paper along the line \[y=x\] then you observe that the graphs are superimposed on one another. And that it looks like only one graph here.
And we can say that a logarithmic function and the inverse of logarithmic function are symmetric with respect to the line \[y=x\].
Example: - Find the inverse of the \[f\left( x \right)={{\log }_{2}}\left( x+3 \right)\].
Ans: Firstly, we have to replace \[f\left( x \right)\] from y and interchange x and y.
\[\begin{align}
  & \Rightarrow y={{\log }_{2}}\left( x+3 \right) \\
 & \Rightarrow x={{\log }_{2}}\left( y+3 \right)------\left( 1 \right) \\
\end{align}\]
Now, we replace y with \[{{f}^{-1}}\left( x \right)\] to get the inverse.
And rewrite the log equation into an exponential equation.
So, conversion we will use this formula:
Log equation \[\to \] Exponential equation
\[{{\log }_{b}}\left( M \right)=N\] \[\Rightarrow M={{b}^{N}}\]
So, if we write the equation (1) in this form, then
\[\begin{align}
  & \Rightarrow x={{\log }_{2}}\left( y+3 \right) \\
 & \Rightarrow {{2}^{x}}=y+3 \\
 & \Rightarrow {{2}^{x}}-3=y \\
 & \because y={{f}^{-1}}\left( x \right) \\
\end{align}\]
So, we can write it as: \[{{2}^{x}}-3={{f}^{-1}}\left( x \right)\]
If we check this by the graph then: -

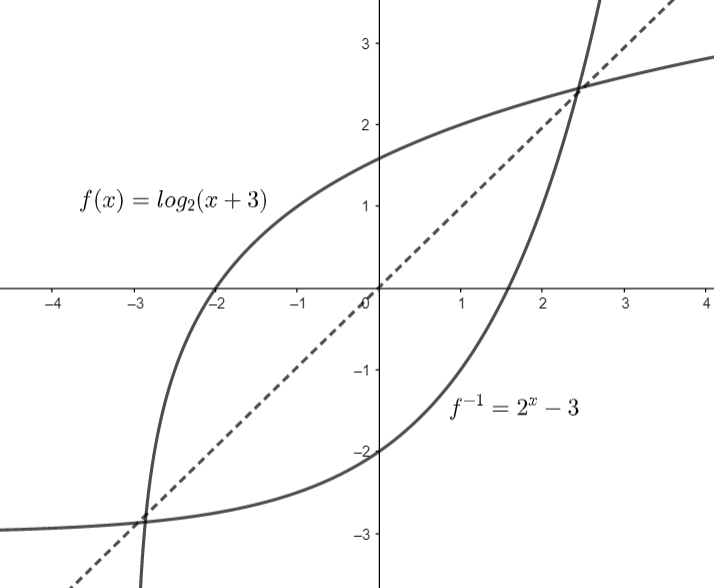
Note: For solving the inverse of any logarithmic function you should be careful during taking anti log and during putting the values and interchanging the coefficients. Because if anyone steps will be wrong then our all the questions will be wrong completely. And the graph will not be symmetrical.