Question

Is 2352 a perfect square? If not, find the smallest number that should be multiplied to 2352 to make a perfect square. Find the square root of the new numbers.

Answer 1

Hint: Prime factorize the given number and check whether each of the prime can be paired or not. If each of the prime factors can be paired then the number will be a perfect square. If not, then multiply by prime factors such that each of them can be paired.

Complete step-by-step solution -

A number is called a perfect square if it can be written as the product of any number multiplied by itself.
Given number is 2352.
Prime factorization of 2352;

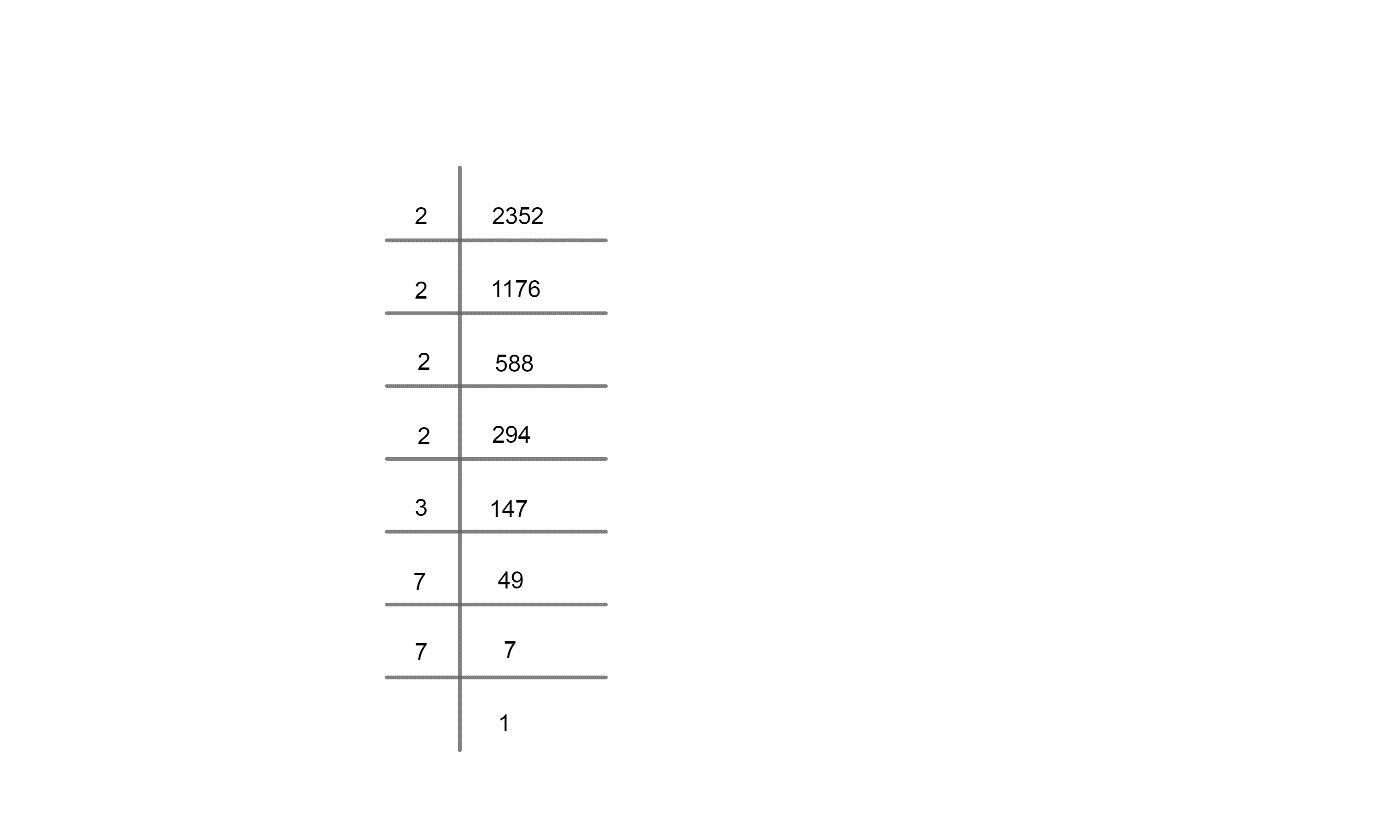
Step 1: Write all the prime factors together,
i.e. \[2352=2\times 2\times 2\times 2\times 3\times 7\times 7\]
Step 2: Make pairs of the same numbers.
\[\times \times \times \]
Now, we can see that each of the numbers except 3 can be paired.
This is not a perfect square because ‘3’ is left unpaired.
To make it a perfect square, we need to make a pair of this remaining 3.
So, we need to multiply the given number with 3.
After multiplying by 3, the number and prime factorization will change to,
\[\begin{align}
  & 2352\times 3=\times \times \times \\
 & \Rightarrow 7056=\times \times \times \\
\end{align}\]
Now, for getting square root of this perfect square number,
Step 3: For each pair, take one of the two in the pair to the square root
So, required square root
$\begin{align}
  & =2\times 2\times 3\times 7 \\
 & =84 \\
\end{align}$

Note: If a number has its unit digit ‘2’, it can’t be a perfect square. For a number to be a perfect square, its unit digit must be 1 or 4 or 6 or 9 or 5.