Question

Is AAS congruence criterion is same as ASA congruence criterion?
(a) True
(b) False

Answer 1

Hint: To solve this problem we need to know what do we mean by congruent triangles. So according to its definition, when two triangles are congruent they will have exactly the same three sides and exactly the same three angles. And AAS and ASA are the properties through which we can prove the two triangles congruent if they are congruent. ASA stands for "angle, side, angle" and means that we have two triangles where we know two angles and the included side are equal. And AAS stands for "angle, angle, side" and means that we have two triangles where we know two angles and the non-included side are equal. We will take an example of two triangles and prove them congruent using both properties and will see if they are the same.

Complete step by step answer:
We have to find if the AAS congruence criterion is same as ASA congruence so for that we need to know what do we mean by congruent triangles first,
Two triangles are congruent if they have all three same angles as well as same sides.
AAS and ASA are methods through which we can prove if two triangles are congruent.
So to check if both the methods are same we will take one example of two triangles and prove them congruent using both methods and check if both the methods are same,
So consider the two triangles as shown in the below figure,

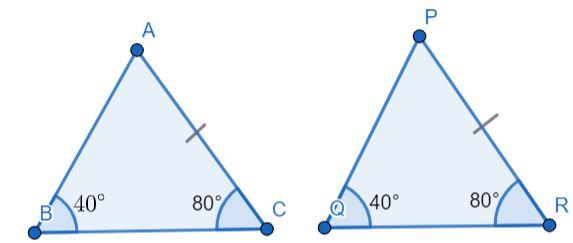
Consider we are given that,
$\begin{align}
  & \angle B=\angle Q \\
 & \angle C=\angle R \\
 & AC=PR \\
\end{align}$
First we will prove using ASA congruence criterion as,
According to ASA condition two triangles are congruent if two angles and included side between them is equal,
Using angle sum property in $\Delta ABC$, we get
\[\begin{align}
  & \angle A+\angle B+\angle C={{180}^{\circ }} \\
 & \angle A+{{40}^{\circ }}+{{80}^{\circ }}={{180}^{\circ }} \\
 & \angle A+{{120}^{\circ }}={{180}^{\circ }} \\
 & \angle A={{180}^{\circ }}-{{120}^{\circ }} \\
 & \angle A={{60}^{\circ }} \\
\end{align}\]
Similarly using angle sum property in $\Delta PRQ$, we get
\[\begin{align}
  & \angle P+\angle Q+\angle R={{180}^{\circ }} \\
 & \angle P+{{40}^{\circ }}+{{80}^{\circ }}={{180}^{\circ }} \\
 & \angle P+{{120}^{\circ }}={{180}^{\circ }} \\
 & \angle P={{180}^{\circ }}-{{120}^{\circ }} \\
 & \angle P={{60}^{\circ }} \\
\end{align}\]
Now in $\Delta ABC\,\,and\,\,\Delta PQR$,
$\begin{align}
  & \angle A=\angle P\,\,\,\left( both\,\,{{60}^{\circ }} \right) \\
 & AC=PR\,\,\,\,\left( given \right) \\
 & \angle C=\angle R\,\,\,\left( both\,\,{{80}^{\circ }} \right) \\
 & hence\,\,\Delta ABC\cong \Delta PQR\,\,\,\,\left( ASA\,congruence\,rule \right) \\
\end{align}$
Now using AAS we have,
In $\Delta ABC\,\,and\,\,\Delta PQR$,
$\begin{align}
  & \angle B=\angle Q\,\,\,\left( both\,\,{{40}^{\circ }} \right) \\
 & \angle C=\angle R\,\,\,\left( both\,\,{{80}^{\circ }} \right) \\
 & AC=PR\,\,\,\,\left( given \right) \\
 & hence\,\,\Delta ABC\cong \Delta PQR\,\,\,\,\left( \operatorname{AAS}\,congruence\,rule \right) \\
\end{align}$
Hence we can see that conditions that we used to prove both triangles congruent by ASA and AAS method are different

So, the correct answer is “False”.

Note: You should note that in ASA criterion that side of the triangles is compared which in between both the compared angles and in the AAS criterion side that is compared is adjacent to any of the respective angles that are being compared. Also try to remember the definitions of congruent triangles as well as mentioned congruence methods.