Question

Is an isosceles triangle always, sometimes or never a right triangle?

Answer 1

Hint: A right triangle is a triangle where the measure of one angle is equal to \[{90^ \circ }\]. An isosceles triangle is a triangle where two sides are equal in length or where two angles have equal measure. An isosceles triangle is a right triangle where the measure of one angle is \[{90^ \circ }\] and the measure of the other two angles are equal. We will see whether an isosceles triangle can be a right triangle or not and if it can be then, is it always or sometimes.

Complete step-by-step answer:
Let us consider that an isosceles triangle is always a right triangle.
So, for a right triangle an angle needs to be equal to \[{90^ \circ }\]. And, for an isosceles triangle, the measure of two angles need to be equal. Let us consider a diagram.

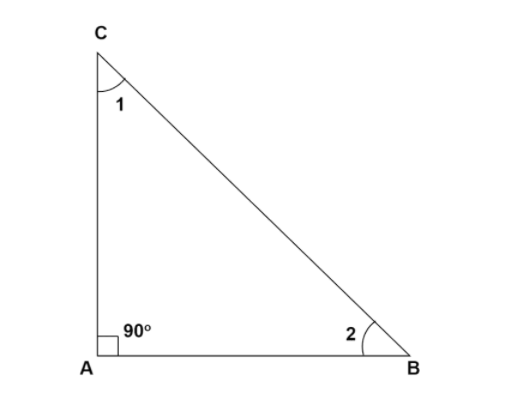
\[\vartriangle ABC\] is a right triangle which is right angled at \[A\].
For a triangle to be an isosceles triangle, two angles need to be equal.
Let \[\angle 1 = \angle 2 - - - - - - (1)\]
Using Angle Sum Property, i.e. Sum of all the angles in a triangle \[ = {180^ \circ }\], we have
\[ \Rightarrow \angle 1 + \angle 2 + \angle A = {180^ \circ }\]
Using (1), we have
\[ \Rightarrow \angle 1 + \angle 1 + {90^ \circ } = {180^ \circ }\]
Solving the left hand side, we have
\[ \Rightarrow 2\angle 1 + {90^ \circ } = {180^ \circ }\]
Reshuffling the terms, we get
\[ \Rightarrow 2\angle 1 = {180^ \circ } - {90^ \circ }\]
\[ \Rightarrow 2\angle 1 = {90^ \circ }\]
Now, Dividing the whole equation by \[2\], we get
\[ \Rightarrow \dfrac{{2\angle 1}}{2} = \dfrac{{{{90}^ \circ }}}{2}\]
\[ \Rightarrow \angle 1 = {45^ \circ }\]
Hence, we have,
\[\angle 1 = \angle 2 = {45^ \circ }\]
Hence, an isosceles triangle is a right triangle if the measure of each of two angles other than the right angle is equal to \[{45^ \circ }\].
But this is not always true that an isosceles triangle is a right triangle.
Let us draw a diagram

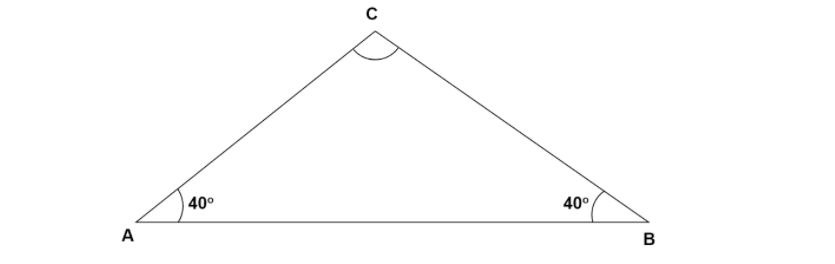
Let us consider a case where
\[\angle A = \angle B = {40^ \circ }\], which implies
\[\angle B + \angle A + \angle C = {180^ \circ }\], using angle sum property
 Substituting \[\angle A = \angle B = {40^ \circ }\], we get
\[ \Rightarrow {40^ \circ } + {40^ \circ } + \angle C = {180^ \circ }\]
Solving the Left Hand side, we get
\[ \Rightarrow {80^ \circ } + \angle C = {180^ \circ }\]
Reshuffling the terms, we get
\[ \Rightarrow \angle C = {180^ \circ } - {80^ \circ }\]
\[ \Rightarrow \angle C = {100^ \circ }\]
Hence, we get
\[\angle A = \angle B = {40^ \circ }\] and \[\angle C = {100^ \circ }\]

Now, we see that this triangle is an isosceles triangle but not a right triangle.
Hence, we can conclude that it is not always true that an isosceles triangle is a right triangle but An isosceles triangle is a right triangle if measure of one angle is equal to \[{90^ \circ }\] and measure of each of the other two angles is \[{45^ \circ }\]. Since, an isosceles triangle can be a right triangle sometimes, then the third case i.e. an isosceles triangle can never be a right triangle is discarded.
Therefore, we can say that an isosceles triangle can be a right triangle sometimes.
So, the correct answer is “sometimes”.

Note: We need to consider every case to answer this question. We need to consider the conditions for both the triangles. None of the conditions can be relaxed. We can also consider the case where measure of each of two angles is \[{90^ \circ }\] but that is not possible as when we apply angle sum property, we will get the measure of third angle to be equal to \[{0^ \circ }\], which means that triangle is not formed.