Question

Is circle an ellipse?

Answer 1

Hint: We are asked if a circle is an ellipse. An ellipse is a geometry which can be said to be formed by the intersection of a plane with a right circular cone and it has two radii associated with it. The equation for ellipse is, \[\dfrac{{{(x-h)}^{2}}}{{{a}^{2}}}+\dfrac{{{(y-k)}^{2}}}{{{b}^{2}}}=1\]. The circle has only one radius and its equations can be written as, \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]. Clearly, we can see that the circle is a special case of an ellipse.

Complete step-by-step solution:
According to the question given to us, we have a circle which we have to tell if it is an ellipse or not.
We know that a circle is a geometry that has a set of points and those points are at a fixed distance from the center point. That is, a circle has only one fixed radius.
The general equation of the circle, centered at \[(h,k)\] having radius r can be written as,
\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

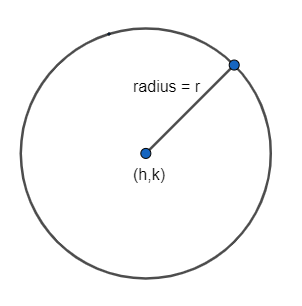
The length of the line from the circumference of the circle to the opposite side of the circle via the center is \[2r\] and that line is called the diameter.
An ellipse on the other hand can be described as a shape formed by the intersection of a plane with a right circular cone and it has two radii associated with it, which is the length on the major and minor axis. The general equation of the ellipse centered at \[(h,k)\] and coordinate on major and minor axis ‘a’ and ‘b’ respectively, \[\dfrac{{{(x-h)}^{2}}}{{{a}^{2}}}+\dfrac{{{(y-k)}^{2}}}{{{b}^{2}}}=1\]

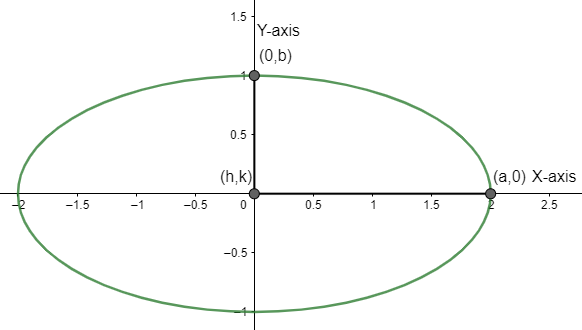
If we compare both the equation of circle as well as the equation of ellipse, we can clearly see that circle is a special case of ellipse when both the major and minor axis have the same coordinate or are equidistant from the centre, then in that case the equation of the ellipse will become,
\[\dfrac{{{(x-h)}^{2}}}{{{a}^{2}}}+\dfrac{{{(y-k)}^{2}}}{{{b}^{2}}}=1\]
\[\Rightarrow \dfrac{{{(x-h)}^{2}}}{{{a}^{2}}}+\dfrac{{{(y-k)}^{2}}}{{{a}^{2}}}=1\] (since \[a=b\])
\[\Rightarrow \dfrac{{{(x-h)}^{2}}}{{{a}^{2}}}+\dfrac{{{(y-k)}^{2}}}{{{a}^{2}}}=1\]
\[\Rightarrow \dfrac{{{(x-h)}^{2}}+{{(y-k)}^{2}}}{{{a}^{2}}}=1\]
\[\Rightarrow {{(x-h)}^{2}}+{{(y-k)}^{2}}={{a}^{2}}\] which is nothing but the equation of circle.
Therefore, a circle is an ellipse.

Note: In the above solution, we have shown that a circle is an ellipse, but the converse of it is not correct, that is, an ellipse is a circle. An ellipse cannot be a circle as a circle is equidistant from the circumference and rules out the possibility of forming an ellipse which has two radii.