
Is it possible to construct a triangle with sides 9 cm, 6 cm and 17 cm? If not, why?
Answer
525k+ views
Hint: As we can see, 9+6 = 15 which is less than the third side. We know that if the sum of the two smaller sides is equal or more than the third side then the construction of the triangle is possible, but here the sum is less so the triangle cannot be constructed.
Complete step-by-step answer:
We know that the sum of any 2 sides of a triangle should be greater than the third side.
Let A=9 cm, B=6 cm and C=17 cm.
So, here
A+B should be greater than C
Now, A+B= 9+6=15 cm
C=17 cm
Since,
The construction of the given triangle is not possible.
So, in this question construction of a triangle is not possible with sides A=9 cm, B=6 cm and C=17 cm.
Note: It is possible to draw more than one triangle that has three sides with the given lengths. For example, in the figure below, given the base AB, you can draw four triangles that meet the requirements. All four are correct in that they satisfy the requirements, and are congruent to each other.
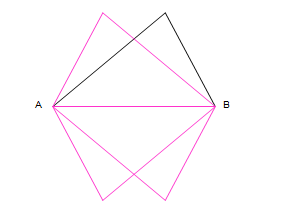
But construction is not always possible, if two sides add to less than the third, no triangle is possible.
Complete step-by-step answer:
We know that the sum of any 2 sides of a triangle should be greater than the third side.
Let A=9 cm, B=6 cm and C=17 cm.
So, here
A+B should be greater than C
Now, A+B= 9+6=15 cm
C=17 cm
Since,
The construction of the given triangle is not possible.
So, in this question construction of a triangle is not possible with sides A=9 cm, B=6 cm and C=17 cm.
Note: It is possible to draw more than one triangle that has three sides with the given lengths. For example, in the figure below, given the base AB, you can draw four triangles that meet the requirements. All four are correct in that they satisfy the requirements, and are congruent to each other.

But construction is not always possible, if two sides add to less than the third, no triangle is possible.
Recently Updated Pages
Out of 30 students in a class 6 like football 12 like class 7 maths CBSE

Earth rotates from West to east ATrue BFalse class 6 social science CBSE

The easternmost longitude of India is A 97circ 25E class 6 social science CBSE

Write the given sentence in the passive voice Ann cant class 6 CBSE

Convert 1 foot into meters A030 meter B03048 meter-class-6-maths-CBSE

What is the LCM of 30 and 40 class 6 maths CBSE

Trending doubts
Give 10 examples for herbs , shrubs , climbers , creepers

How many millions make a billion class 6 maths CBSE

The forces of Alexander and Porus fought on the banks class 6 social science CBSE

Number of Prime between 1 to 100 is class 6 maths CBSE

Four bells toll together at 900am They toll after 7811 class 6 maths CBSE

What is the full form of AD a After death b Anno domini class 6 social science CBSE





