
How is the kinetic energy versus temperature graph for a given substance?

Answer
480.3k+ views
1 likes
Hint: Write the relationship between the average kinetic energy of the molecules and absolute temperature. From this relationship, decide if the plot is a straight line or a curve. For a curve, decide the shape of the curve from the relationship. If a straight line is obtained, then decide if the slope is positive or negative.
Complete Step by step answer: The average kinetic energy of the molecules is
Here,
Thus, the average kinetic energy of the molecules is directly proportional to the absolute temperature.
At absolute zero, the average kinetic energy of the molecules has a value of zero. With increase in the absolute temperature, the average kinetic energy of the molecules also increases.
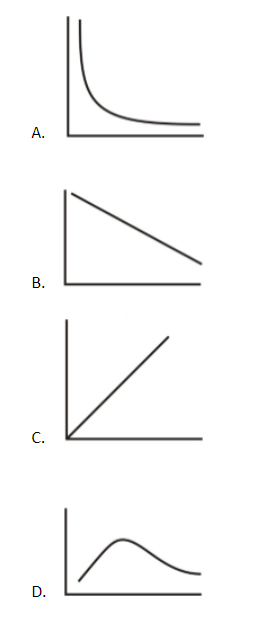
For one mole of the ideal gas, the average molecular kinetic energy of molecules is plotted on the Y axis whereas the absolute temperature is plotted on the X axis. The plot is a straight line passing through the origin and having a positive slope. Such a plot is obtained in the plot of the option (C).
Hence, the correct option is the option (C).
Note: We should note that the kinetic energy is expressed in terms of temperature and not the velocity. So we can also say that there would be relation in between the temperature and the velocity of molecules.The Boltzmann constant
Complete Step by step answer: The average kinetic energy of the molecules is
Here,
Thus, the average kinetic energy of the molecules is directly proportional to the absolute temperature.
At absolute zero, the average kinetic energy of the molecules has a value of zero. With increase in the absolute temperature, the average kinetic energy of the molecules also increases.
For one mole of the ideal gas, the average molecular kinetic energy of molecules is plotted on the Y axis whereas the absolute temperature is plotted on the X axis. The plot is a straight line passing through the origin and having a positive slope. Such a plot is obtained in the plot of the option (C).
Hence, the correct option is the option (C).
Note: We should note that the kinetic energy is expressed in terms of temperature and not the velocity. So we can also say that there would be relation in between the temperature and the velocity of molecules.The Boltzmann constant
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




