Question

What kVA rating is required for a transformer that must handle a maximum load current of 8A with a secondary voltage of 2 kV?
A) 4kVA
B) 0.25kVA
C) 16kVA
D) 8kVA

Answer 1

Hint:
A volt-ampere is the unit used for the apparent power in an electrical circuit. The apparent power equals the product of volt and current in ampere.
When we wants to measure it in a higher unit that is called kVA means kilo volt-ampere
Which is given by formula
$kVA = \dfrac{{Volt \times Amps}}{{1000}}$

Complete step by step answer:
A kVA is 1,000 volt-amps. It's what you get when you multiply the voltage by the amps (electrical current). Kilovolt-amps measure what's called the 'apparent power' of a transformer.
As shown in the diagram, the transformer has two coils: primary coil and secondary coil.

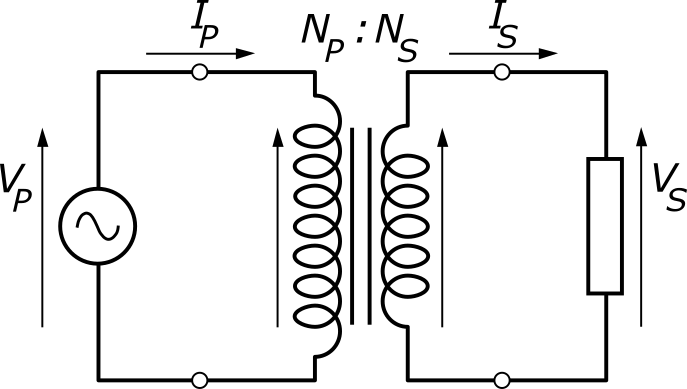
In primary coil input AC voltage is ${V_p}$ and current is ${I_p}$ and in secondary coil found the voltage ${V_s}$ and current ${I_s}$ then the apparent power of this transformer can be defined by the given formula
$ \Rightarrow kVA = \dfrac{{{V_p} \times {I_p}}}{{1000}} = \dfrac{{{V_s} \times {I_s}}}{{1000}}$
Means the power in primary coil is always equal to the power in secondary coil. By using this formula we can calculate the kVA of any transformer or can calculate the current or voltage in primary or secondary coil.
In this question given ${I_s} = 8A$
And voltage in secondary coil ${V_s} = 2kV$
We know $1kV = 1000V$
So ${V_s} = 2000V$
Put these value in given formula then
$ \Rightarrow kVA = \dfrac{{2000 \times 8}}{{1000}}$
$ \Rightarrow kVA = \dfrac{{16000}}{{1000}}$
Further solving we get.
$\therefore kVA = 16$
$\therefore $ Apparent power of this transformer or kVA rating is $ = 16kVA$

therefore In this question option C is correct.

Note:Here we use formula for single phase transformer if in the question the given transformer is three phase transformer then multiply this formula by $\sqrt 3 $ then we get a new formula for three phase transformer which is $ \Rightarrow kVA = \dfrac{{\sqrt 3 \times {V_p} \times {I_p}}}{{1000}} = \dfrac{{\sqrt 3 \times {V_s} \times {I_s}}}{{1000}}$