
What is the length of the common chord of two circles of radii 15 cm and 20 cm whose centres are 25 cm apart?
A. 24
B. 15
C. 12
D. none of the above
Answer
515.8k+ views
Hint: In order to solve this problem you need to draw the figure and use some of the properties of circle that radius is always perpendicular to any chord of the circle, if two circles have common chords then they intersects at two points and then we need to apply the Pythagoras theorem in the triangle formed since all the lengths are given. Doing this will solve your problem.
Complete step by step answer:
It is given that two circles of radii 15 cm and 20 cm whose centre are 25 cm apart and they have a common chord we need to find the length of that chord.
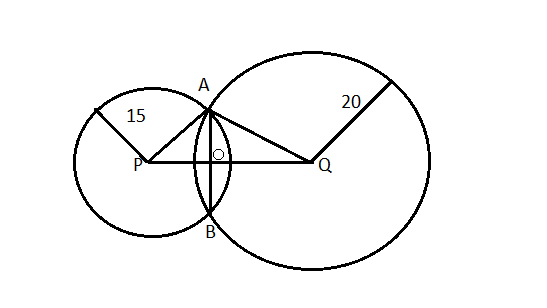
Above is the diagram of the two circles having a common chord and we know that it's perpendicular to the line joining P and Q that is PQ is perpendicular. We need to find the length of chord AB.
As we know PQ is perpendicular bisector of AB so AO = OB……(1)
So, we will apply Pythagoras theorem to get the value of PO to get the value of AO to get the right answer.
It is given that PQ = 25cm
Let PO = x, then QO = 25 – x.
Applying Pythagoras in Triangle AOP we get,
$
\Rightarrow A{O^2} = A{P^2} - O{P^2} \\
\Rightarrow A{O^2} = {15^2} - {x^2}.........(2) \\
$
Again applying Pythagoras in triangle AOQ we get,
$
\Rightarrow A{O^2} = A{Q^2} - O{Q^2} \\
\Rightarrow A{O^2} = {15^2} - {\left( {25 - x} \right)^2}.........(3) \\
$
From (2) and (3) we can say that,
$
{20^2} - {\left( {25 - x} \right)^2} = {15^2} - {x^2} \\
400 - 625 - {x^2} + 50x = 225 - {x^2} \\
50x = 450 \\
x = 9 \\
$
So, PO = 9cm then OQ = 16cm
Now we can apply the Pythagoras theorem in any of the triangle AOP or AOQ to get the value of AO.
So, we do,
$ \Rightarrow A{O^2} = A{P^2} - O{P^2}$
Putting the values we get,
\[
\Rightarrow A{O^2} = {15^2} - {9^2} \\
\Rightarrow A{O^2} = 225 - 81 \\
\Rightarrow A{O^2} = 144 \\
\Rightarrow AO = 12cm \\
\]
So, we get AO = 12cm we know that AB = 2AO from (1)
So, the length of the chord AB = 2(12) = 24cm.
So, the correct answer is “Option A”.
Note: In this problem we have used various properties of a circle like the common chord is perpendicularly bisected by the line joining the centers of the two circles and then we have applied the Pythagoras theorem in the various triangles formed in the figure to get the right answer. Drawing the figure will help you a lot in such types of problems.
Complete step by step answer:
It is given that two circles of radii 15 cm and 20 cm whose centre are 25 cm apart and they have a common chord we need to find the length of that chord.
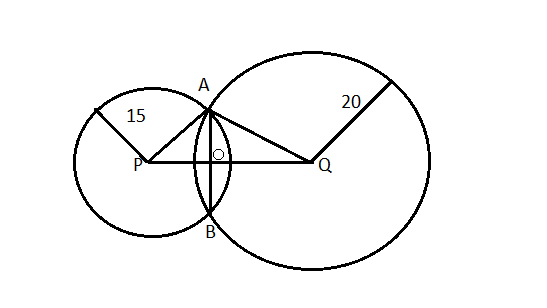
Above is the diagram of the two circles having a common chord and we know that it's perpendicular to the line joining P and Q that is PQ is perpendicular. We need to find the length of chord AB.
As we know PQ is perpendicular bisector of AB so AO = OB……(1)
So, we will apply Pythagoras theorem to get the value of PO to get the value of AO to get the right answer.
It is given that PQ = 25cm
Let PO = x, then QO = 25 – x.
Applying Pythagoras in Triangle AOP we get,
$
\Rightarrow A{O^2} = A{P^2} - O{P^2} \\
\Rightarrow A{O^2} = {15^2} - {x^2}.........(2) \\
$
Again applying Pythagoras in triangle AOQ we get,
$
\Rightarrow A{O^2} = A{Q^2} - O{Q^2} \\
\Rightarrow A{O^2} = {15^2} - {\left( {25 - x} \right)^2}.........(3) \\
$
From (2) and (3) we can say that,
$
{20^2} - {\left( {25 - x} \right)^2} = {15^2} - {x^2} \\
400 - 625 - {x^2} + 50x = 225 - {x^2} \\
50x = 450 \\
x = 9 \\
$
So, PO = 9cm then OQ = 16cm
Now we can apply the Pythagoras theorem in any of the triangle AOP or AOQ to get the value of AO.
So, we do,
$ \Rightarrow A{O^2} = A{P^2} - O{P^2}$
Putting the values we get,
\[
\Rightarrow A{O^2} = {15^2} - {9^2} \\
\Rightarrow A{O^2} = 225 - 81 \\
\Rightarrow A{O^2} = 144 \\
\Rightarrow AO = 12cm \\
\]
So, we get AO = 12cm we know that AB = 2AO from (1)
So, the length of the chord AB = 2(12) = 24cm.
So, the correct answer is “Option A”.
Note: In this problem we have used various properties of a circle like the common chord is perpendicularly bisected by the line joining the centers of the two circles and then we have applied the Pythagoras theorem in the various triangles formed in the figure to get the right answer. Drawing the figure will help you a lot in such types of problems.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

State and prove the Pythagoras theorem-class-10-maths-CBSE

A Gulab jamun contains sugar syrup up to about 30 of class 10 maths CBSE

What is UltraEdge (Snickometer) used for in cricket?

What are the public facilities provided by the government? Also explain each facility

Distinguish between the reserved forests and protected class 10 biology CBSE




