Question

Let A = (1, 2, 3) and B = (a, b, c). If $f$ is a function from A to B and $g$ is a one-one function from A to B, then the maximum number of definitions of:
(a) $f$ is 9
(b) $g$ is 9
(c) $f$ is 27
(d) $g$ is 6

Answer 1

Hint: If a set A has $n$ elements and set B has $m$ elements and if $f$ is a function from A to B then maximum number of mappings from A to B is given by the formula ${{n}^{m}}$ or we can say maximum number of definitions of $f$ is ${{n}^{m}}$.

Complete step-by-step answer:
First we should understand what is a function and its difference with relation and then we will know about one-one function which is a type of function.
A function is a relation which describes that there should be only one output for each input. Now, a relation is a set of inputs and outputs that are related in some way. The basic difference between a relation and a function is that, when each input in a relation has exactly one output, the relation is said to be a function. However one output may be related to several inputs. If we want to check if a relation is a function or not, we check that no input has more than one output.
Now, there are different types of functions and here we have to see only one-one functions. One-one function can be defined as a function that maps distinct elements of its domain to distinct elements of its co-domain or range. In the above question elements of set A are domains and elements of set B are co-domains or range. One-one function is also called an injective function.

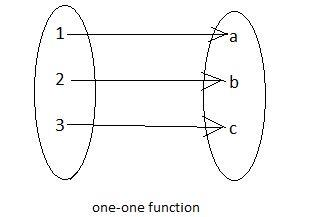
Now, consider set A = (1, 2, 3) and set B = (a, b, c).
f is a function from A to B
$\therefore $Maximum number of definitions of $f$ = ${{3}^{3}}$ = 27, since both sets have 3 elements.

Also, $g$ is a one-one function from A to B, so each element of set A is related to only one element of set B. So, we cannot use ${{n}^{m}}$ here and therefore, we need to take a different approach. We can see that element (a) can be mapped by one of the three elements (1, 2 or 3). So, there are three ways to map (a). Now once (a) is mapped only two elements in both the sets are remaining. So, let us map (b) next and it can be mapped by either of the two elements remaining in set A, so, there will be 2 ways to map (b). Now only one element is left in both the sets and there will be only one way to map.
$\therefore $Maximum number of definitions of $g$ = $3\times 2\times 1$ = $6$.
Hence, option (c) and (d) are correct.

Note: We should learn and understand the concepts of functions and its difference with relations. Types of functions are an important topic to discuss. The main difficulty we may face while thinking over this question is two different approaches for two different situations. In the first situation of the question the function from A to B was not one-one but in the second situation it was for $g$.