Question

Let \[{A_0},{\text{ }}{A_1},{\text{ }}{A_2},{\text{ }}{A_3},{\text{ }}{A_4},{\text{ }}{A_5}\] be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments \[{A_0}{A_1},{\text{ }}{A_0}{A_2},\] and \[{A_0}{A_4}\] is:
A) $ \dfrac{3}{4} $
B) $ 3\sqrt 3 $
C) $ 3 $
D) $ \dfrac{{3\sqrt 3 }}{2} $

Answer 1

Hint: To solve this problem, we will first construct a figure using the information given to us, then we will find the coordinates of the vertices of the hexagon using the basic properties of it. Afterwards, we will apply the distance formula, since we are asked about the length of the line segment, and hence on putting the values, we will get our required answer. Also don’t forget to take the product of the lengths of the line segments in the end, as that will be our complete answer.

Complete step-by-step answer:
We have been given that \[{A_0},{\text{ }}{A_1},{\text{ }}{A_2},{\text{ }}{A_3},{\text{ }}{A_4},{\text{ }}{A_5}\] be the vertex of a regular hexagon inscribed in a circle of unit radius. We need to find the product of the lengths of the line segments \[{A_0}{A_1},{\text{ }}{A_0}{A_2},\] and \[{A_0}{A_4}.\]
Let us construct a figure using the above information.
 

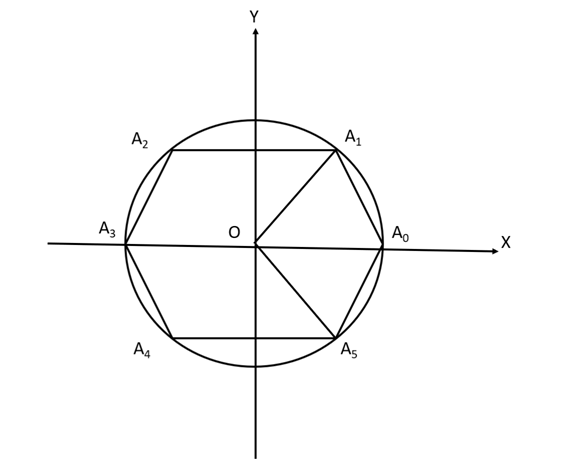
Here, \[O{A_0}\] is a radius of the circle. So according to the question it is equal to one.
Then, \[O{A_0} = {\text{ }}O{A_1} = {\text{ }}O{A_2} = {\text{ }}O{A_3} = {\text{ }}O{A_4} = {\text{ }}O{A_5} = {\text{ }}O{A_6} = {\text{ }}1\]
We know that a regular hexagon has all sides equal. And, we also know that each side of the hexagon makes an angle \[60^\circ \] at the centre.
So, using this information we will get the coordinates of \[{A_0},{\text{ }}{A_1},{\text{ }}{A_2},{\text{ }}{A_3},{\text{ }}{A_4}\] and \[{A_5}\] which are mentioned below.
\[{A_0} = {\text{ }}\left( {1,0} \right)\]
\[{A_1} = {\text{ }}(cos60^\circ ,sin60^\circ ){\text{ }} = {\text{ }}(\dfrac{1}{2},\dfrac{{\sqrt 3 }}{2})\]
\[{A_2} = {\text{ }}(cos120^\circ ,sin120^\circ ){\text{ }} = {\text{ }}(\dfrac{{ - 1}}{2},\dfrac{{\sqrt 3 }}{2})\]
\[{A_3} = {\text{ }}\left( { - 1,0} \right)\]
\[{A_4} = {\text{ }}( - cos60^\circ , - sin60^\circ ){\text{ }} = {\text{ }}(\dfrac{{ - 1}}{2},\dfrac{{ - \sqrt 3 }}{2})\]
\[{A_5} = {\text{ }}( - cos120^\circ , - sin120^\circ ){\text{ }} = {\text{ }}(\dfrac{1}{2},\dfrac{{ - \sqrt 3 }}{2})\]

Now to find the length of the line segments we will use the distance formula, for that we will use the formula mentioned below.
Distance formula \[ = {\text{ }}\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
\[{\left( {{A_0}{A_1}} \right)^2} = {\text{ }}{\left( {\dfrac{1}{2} - 1} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2} - 0} \right)^2}\]
\[
{\left( {{A_0}{A_1}} \right)^2} = {\text{ }}{\left( {\dfrac{1}{2} - 1} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2} - 0} \right)^2} \\
{\left( {{A_0}{A_1}} \right)^2} = {\text{ }}{\left( {\dfrac{{ - 1}}{2}} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2}} \right)^2} = {\text{ }}\left( {\dfrac{1}{4}} \right) + \left( {\dfrac{3}{4}} \right) = \dfrac{4}{4} = 1 \\
 \]
\[ \Rightarrow {A_0}{A_1} = {\text{ }}1\]
Now, \[{\left( {{A_0}{A_2}} \right)^2} = {\text{ }}{\left( { - \dfrac{1}{2} - 1} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2} - 0} \right)^2}\]
\[
{\left( {{A_0}{A_2}} \right)^2} = {\text{ }}{\left( {\dfrac{{ - 3}}{2}} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2}} \right)^2} = {\text{ }}\left( {\dfrac{9}{4}} \right) + \left( {\dfrac{3}{4}} \right) = \dfrac{{12}}{4} = 3 \\
\Rightarrow {A_0}{A_2} = \sqrt 3 \\
 \]
And, \[{\left( {{A_0}{A_4}} \right)^2} = {\left( {\dfrac{{ - 1}}{2} - 1} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2} - 0} \right)^2}\]
\[
{\left( {{A_0}{A_4}} \right)^2} = {\left( {\dfrac{{ - 3}}{2}} \right)^2} + {\left( {\dfrac{{\sqrt 3 }}{2}} \right)^2} = \left( {\dfrac{9}{4}} \right) + \left( {\dfrac{3}{4}} \right) = \dfrac{{12}}{4} = 3 \\
\Rightarrow {A_0}{A_4} = \sqrt 3 \\
 \]
Now, the product of the lengths of the line segments \[{A_0}{A_1},{\text{ }}{A_0}{A_2}\] and \[{A_0}{A_4}\]\[\; = 1 \times \sqrt 3 \times \sqrt 3 = 3\]

So, the correct answer is “Option C”.

Note: Students, should note that in the solutions we have taken coordinates of \[{A_0}\] and \[{A_3}\] as \[\left( {1,0} \right)\] and \[\left( { - 1,0} \right)\] respectively, because both the vertices are in the positive and negative x-axis and also the value \[1\] is taken because it is mentioned in the question that the circle has radius equals to unit.