Let ABC be a triangle and M be a point on side AC closer to vertex C than A. Let N be a point on side AB such that MN is parallel to BC and let P be a point on side BC such that MP is parallel to AB. If the area of the quadrilateral BNMP is equal to \[\frac{5}{{18}}\] times the area of triangle ABC, then the ratio AM/MC equals.
A. 5
B. 6
C.$\frac{{18}}{5}$
D.$\frac{{15}}{2}$
Answer
Verified363k+ views
Hint-Make use of the property of similar triangles and try to solve this problem
Using the data given let us draw the figure
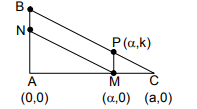
Let us consider the length of AM to be=x and MC =y
Also it is given that MN is parallel to BC, so BN is the transversal
So from this we get $\begin{gathered}
\angle ANM = \angle ABC \\
\angle AMN = \angle ACB \\
\end{gathered} $ (corresponding angles)
And also MP is parallel to NB.
So, we get $\angle ANM = \angle MPC$(Since MP is parallel to BN )
So, from this we can write $\vartriangle ANM \sim \vartriangle MPC \sim \vartriangle ABC$
So by theorem, ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
$\frac{{area\vartriangle ANM}}{{area\vartriangle ABC}} = \frac{{{{(AM)}^2}}}{{{{(AC)}^2}}} = \frac{{{x^2}}}{{{{(x + y)}^2}}}$ ------(1)
$\frac{{area\vartriangle MPC}}{{area\vartriangle ABC}} = \frac{{{{(MC)}^2}}}{{{{(AC)}^2}}} = \frac{{{y^2}}}{{{{(x + y)}^2}}}$----------(2)
From the data it is given that $area\vartriangle ANC + area\vartriangle MPC = area\vartriangle ABC - area\square NMCB = area\vartriangle ABC - \dfrac{5}{{18}}\vartriangle ABC = \dfrac{{13}}{{18}}area\vartriangle ABC$ Now ,let us add eq(1) and eq(2)
So we get
$\begin{gathered}
\frac{{13}}{{18}} = \frac{{{x^2} + {y^2}}}{{{{(x + y)}^2}}} \\
\Rightarrow 5{x^2} - 26xy + 5{y^2} = 0 \\
\Rightarrow 5{x^2} - 25xy - xy + 5{y^2} = 0 \\
\Rightarrow (5x - 1)(x - 5y) = 0 \\
\Rightarrow \frac{x}{y} = 5{\text{ OR }}\frac{x}{y} = \frac{1}{5} \\
\end{gathered} $
But, also it is given that x>y
Therefore the answer is 5
Option A is the correct answer
Note: Modify the equation and bring it to a simplified form based on the data which is given in the question
Using the data given let us draw the figure
Let us consider the length of AM to be=x and MC =y
Also it is given that MN is parallel to BC, so BN is the transversal
So from this we get $\begin{gathered}
\angle ANM = \angle ABC \\
\angle AMN = \angle ACB \\
\end{gathered} $ (corresponding angles)
And also MP is parallel to NB.
So, we get $\angle ANM = \angle MPC$(Since MP is parallel to BN )
So, from this we can write $\vartriangle ANM \sim \vartriangle MPC \sim \vartriangle ABC$
So by theorem, ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
$\frac{{area\vartriangle ANM}}{{area\vartriangle ABC}} = \frac{{{{(AM)}^2}}}{{{{(AC)}^2}}} = \frac{{{x^2}}}{{{{(x + y)}^2}}}$ ------(1)
$\frac{{area\vartriangle MPC}}{{area\vartriangle ABC}} = \frac{{{{(MC)}^2}}}{{{{(AC)}^2}}} = \frac{{{y^2}}}{{{{(x + y)}^2}}}$----------(2)
From the data it is given that $area\vartriangle ANC + area\vartriangle MPC = area\vartriangle ABC - area\square NMCB = area\vartriangle ABC - \dfrac{5}{{18}}\vartriangle ABC = \dfrac{{13}}{{18}}area\vartriangle ABC$ Now ,let us add eq(1) and eq(2)
So we get
$\begin{gathered}
\frac{{13}}{{18}} = \frac{{{x^2} + {y^2}}}{{{{(x + y)}^2}}} \\
\Rightarrow 5{x^2} - 26xy + 5{y^2} = 0 \\
\Rightarrow 5{x^2} - 25xy - xy + 5{y^2} = 0 \\
\Rightarrow (5x - 1)(x - 5y) = 0 \\
\Rightarrow \frac{x}{y} = 5{\text{ OR }}\frac{x}{y} = \frac{1}{5} \\
\end{gathered} $
But, also it is given that x>y
Therefore the answer is 5
Option A is the correct answer
Note: Modify the equation and bring it to a simplified form based on the data which is given in the question
Last updated date: 24th Sep 2023
•
Total views: 363k
•
Views today: 8.63k
Recently Updated Pages
