Question

Let ABC be a triangle whose circumcentre is at P. If the position vectors of A, B, C and P are \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] and $ \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{4} $ respectively, then the position vector of the orthocentre of this triangle, is:
(a) $ -\left( \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{2} \right) $
(b) $ \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} $
(c) $ \dfrac{\left( \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} \right)}{2} $
(d) $ \overrightarrow{0} $

Answer 1

Hint: We start solving the problem by recalling the fact that the centroid of the triangle with position vectors of vertices \[\overrightarrow{p}\], \[\overrightarrow{q}\], \[\overrightarrow{r}\] is $ \dfrac{\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}}{3} $ . We use this fact to find the centroid of the triangle ABC. We then recall the fact that centroid divided the line joining the orthocentre and circumcentre in a ratio of $ 2:1 $ internally. We then make use of the fact that if a point S divides the points Q and R in the ratio of m:n internally, then $ S=\dfrac{mR+nQ}{m+n} $ . We then make the necessary calculations to get the required position vector of the orthocentre.

Complete step by step answer:
According to the problem, we are given that ABC is a triangle whose circumcentre is at P and the position vectors of A, B, C and P are \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] and $ \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{4} $ respectively. We need to find the position vector of the orthocentre of the triangle.

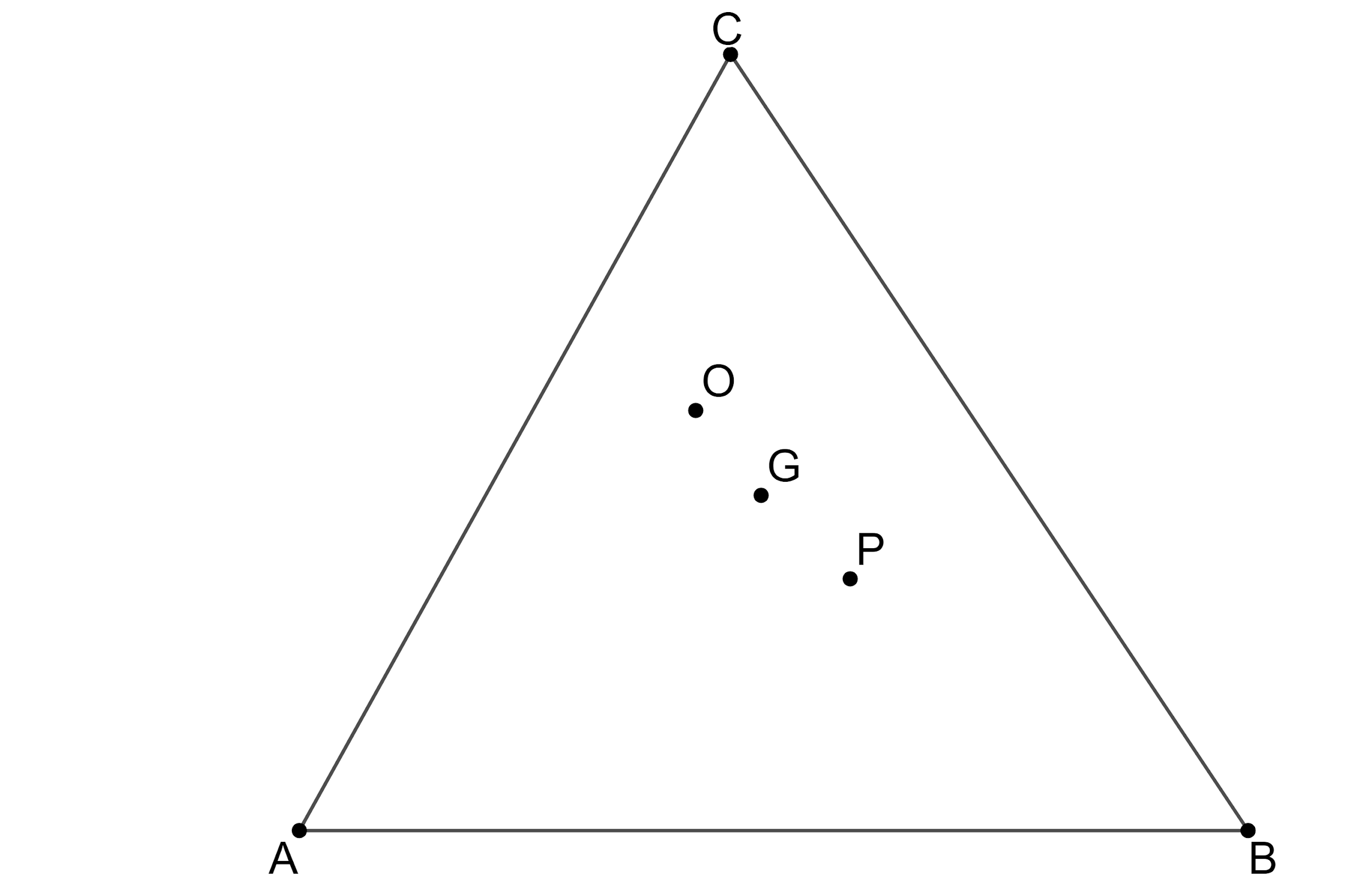
Let us assume ‘G’ be the centroid of the triangle ABC.
We know that the centroid of the triangle with position vectors of vertices \[\overrightarrow{p}\], \[\overrightarrow{q}\], \[\overrightarrow{r}\] is $ \dfrac{\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}}{3} $ .
So, we get the position vector of ‘G’ as $ \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3} $ .
We know that the centroid divided the line joining the orthocentre and circumcentre in a ratio of $ 2:1 $ internally.
Let us assume the orthocentre of the triangle is ‘O’.
We know that if a point S divides the points Q and R in the ratio of m:n internally, then $ S=\dfrac{mR+nQ}{m+n} $ .
So, we get $ G=\dfrac{2P+O}{2+1}\Leftrightarrow G=\dfrac{2P+O}{3} $ .
 $ \Rightarrow 3G=2P+O $ .
 $ \Rightarrow O=3G-2P $ .
Now, let us substitute $ P=\dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{4} $ and $ G=\dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3} $ .
 $ \Rightarrow O=3\left( \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3} \right)-2\left( \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{4} \right) $ .
 $ \Rightarrow O=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-\left( \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{2} \right) $ .
 $ \Rightarrow O=\left( \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{2} \right) $ .
So, we have found the position of orthocentre of the triangle ABC as $ \left( \dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{2} \right) $ .
 $ \therefore, $ The correct option for the given problem is (c).

Note:
We should confuse with the section formula as $ S=\dfrac{mQ+nR}{m+n} $ instead of $ S=\dfrac{mR+nQ}{m+n} $ which is the common mistake done by students. We can also solve the problem by finding the position vectors of altitudes to the sides of the triangle and then finding the intersection to get the required answer. Similarly, we can expect problems to find the position vector of the nine-point center of triangle ABC.