Question

Let C be the mid-point of an arc AB of a circle such that \[m\text{ arc AB}={{183}^{o}}\]. If the region bounded by the arc ACB and line segment AB is denoted by S, then the center O of the circle lies
(a) in the interior of S
(b) in the exterior of S
(c) on the segment AB
(d) on AB and bisects AB

Answer 1

Hint: We have to visualize and draw the diagram with the given details first. Then, we can check if the angle is greater than \[{{180}^{o}}\] or less than \[{{180}^{o}}\] to find the right option.

Complete step-by-step answer:

We have been given in the question that AB is an arc where C is the midpoint of AB. Also, we are given that \[m\text{ arc AB}={{183}^{o}}\]. Let us visualize the given data in picture form.

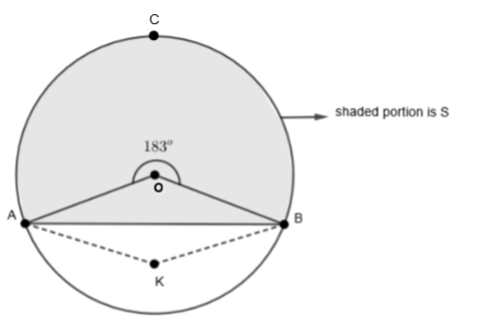
In this picture, the shaded portion is ‘S’. Also, given that the region is bounded by the arc ACB and the line segment AB and is denoted by S. We have already separated the portion of S from the entire circular area. We will now go through options to solve this problem further. Option (a) is the correct answer because from the figure we can see that the center of the circle lies inside surface area ‘S’. \[{{180}^{o}}\] means it is a semi-circle. So, the given angle is \[{{183}^{o}}\]. Hence, the shaded region S will be bigger than a semicircle. So, the center of the circle lies inside the shaded region S.

The rest of the options – (b), (c), and (d) are wrong because the center is lying inside the surface area.


Note: In such a type of question, students must visualize the geometry rather than trying to solve it algebraically. This will save the students’ time greatly. This question might seem tough, but the students must understand that by drawing a figure and marking the relevant details, they can easily solve this question and get full marks for it.