Question

Let $PQ$ be a double ordinate of the parabola, ${y^2} = - 4x$, where $P$ lies in the second quadrant. If $R$ divides $PQ$ in the ratio 2 : 1, then the locus of $R$ is
$
  {\text{A}}{\text{. 3}}{y^2} = - 2x \\
  {\text{B}}{\text{. }}9{y^2} = 4x \\
  {\text{C}}{\text{. }}9{y^2} = - 4x \\
  {\text{D}}{\text{. }}3{y^2} = 2x \\
 $

Answer 1

Hint: In this question, firstly we have to analyse the question and understand the concept of parabola. We have to identify the ratio in which the ordinate is divided and then find its locus by checking all the options one by one.

Complete step-by-step answer:

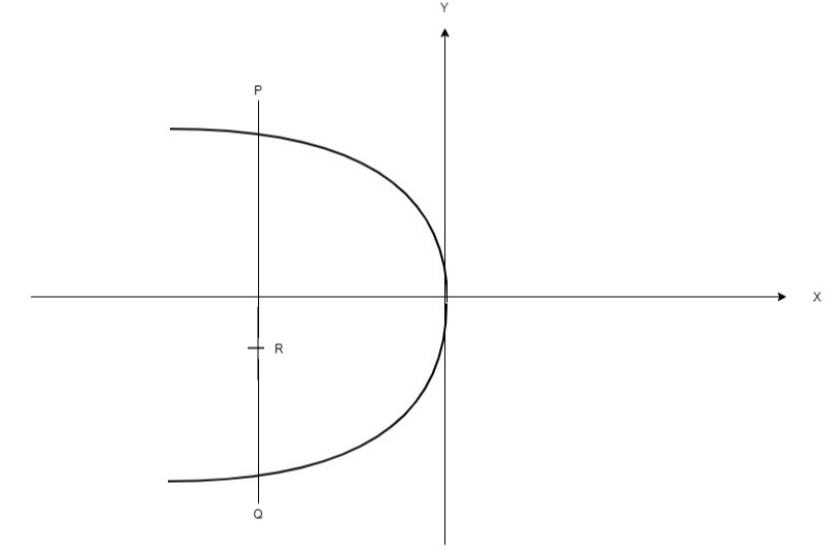
Now assume the coordinates of points ${\text{P,Q & R}}$ as
${\text{P}}\left( { - at_1^2,2a{t_1}} \right),Q\left( { - at_1^2,2a{t_1}} \right)$ and ${\text{R}}\left( {h,k} \right)$
As ${\text{R}}$ divides ${\text{PQ}}$in the ratio 2:1 according to question, we take the coordinates of P & Q in that ratio and equate it with the coordinates of ${\text{R}}$
Then, step 1 is
        $h = \dfrac{{ - 1at_1^2 - 2at_1^2}}{{2 + 1}} = - at_1^2$
and step 2 is
        $k = \dfrac{{1 \times 2a{t_1} - 2 \times 2a{t_1}}}{{2 + 1}} = \dfrac{{ - 2a{t_1}}}{3}$
Now from step 2 we gather the value of ${t_1}$ and put it in step 1. So, we get
$h = - a{\left( {\dfrac{{3k}}{{ - 2a}}} \right)^2} = - \dfrac{{9{k^2}}}{4}$
$ \Rightarrow 9{k^2} = - 4h$ or we can put $x\& y$ in place of $h\& k$
$9{y^2} = - 4x$
Hence, option C is the correct answer.

Note: Whenever we face such types of questions the key point to remember is that any chord that is perpendicular to the axis of parabola is called a double ordinate. So, we have to assume the points on parabola and equate them to the point on double ordinate and then check our options and find the right answer.