Question

Let two like parallel forces be acting, at points $A$ and $B$ such that the force at $A$ is double than the force at $B$. If $C$ is the point of action of the resultant, then $AC/BC$ is
$A)\text{ }2$
$B)\text{ 1/}2$
$C)\text{ 1/3}$
$D)\text{ 1/4}$

Answer 1

Hint: The resultant of the two force vectors must be such that it has the same effect on a body as both the individual vectors combined has. Hence, the resultant must be a force vector that can provide the magnitude and direction of the force and torque that a hypothetical body experiences if subjected to those two force vectors in proper orientation.

Complete step by step answer:
We will find the magnitude, direction and the point of action of the resultant of the two given force vectors. This resultant must have the same effect on a hypothetical body (magnitude and direction of force and torque) that is subjected to the resultant as if it were subjected to the two individual forces together.
Let us draw a diagram to understand the orientation of the force vectors better.

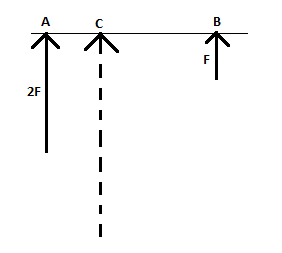
As shown in the figure and according to the question, let the magnitudes of the forces at the points of action $A$ and $B$ be $2F$ and $F$ respectively.
Now, since the two individual forces are like parallel vectors, their resultant will be in the same direction and have a magnitude as the sum of the individual magnitudes.
Hence magnitude $R$ of resultant will be
$R=2F+F=3F$ --(1)
This is so that the resultant has the same force effect on a hypothetical body as the two individual forces.
Now, we will try to get the position of $C$ such that the total torque produced on a hypothetical body due to the two individual forces is equal in magnitude and direction to the torque produced by the resultant alone.
Hence, let us find the torque ${{\tau }_{i}}$ due to the two forces about $C$.
${{\tau }_{i}}=-2F\left( AC \right)+F\left( BC \right)$ (Considering counterclockwise torques as positive)
$\therefore {{\tau }_{i}}=F\left( -2AC+BC \right)$ --(2)
Now, the torque ${{\tau }_{R}}$ due to the resultant at $C$ will be
${{\tau }_{R}}=3F\left( 0 \right)=0$ --(3)
 (Since, the resultant acts at the point about which the torque has to be found out, it has a perpendicular distance of zero from the point and hence provides zero torque).
As explained earlier,
${{\tau }_{i}}={{\tau }_{R}}$
Therefore, using (2) and (3), we get,
$F\left( -2AC+BC \right)=0$
$\therefore -2AC+BC=0$ $\left( \because F\ne 0\text{ as it is given that the force vectors have some non-zero magnitude} \right)$
$\therefore BC=2AC$
$\therefore \dfrac{AC}{BC}=\dfrac{1}{2}$
Hence, the required ratio of $AC/BC$ is $\dfrac{1}{2}$.
Hence, the correct option is $B)\text{ }1/2$

Note: In this problem we see that it is a futile process of finding out the magnitude of the resultant as it gets cancelled when the torque about the point of action of the resultant is being calculated. However, this is only true if the student decides to find the torque about the point of action of the resultant. If the student had chosen any other point, then the magnitude of the resultant would have been necessary. Hence, there are some clever shortcuts that can save time while solving a problem and students must keep note of this clever tactic for future use, especially in competitive examinations.