Question

Let $\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)=l$ and \[\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\tan x} \right)=m\], then
(a) l exists but m does not
(b) m exists but l does not
(c) l and m both exist
(d) neither l nor m exists

Answer 1

Hint: Relate the relation between x, sin x and tan x when x is limiting to zero. Relate it with the domain of \[{{\sec }^{-1}}x\] for existing limits.

Here, we have given the limits as
$\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)=l....\left( i \right)$
And, \[\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\tan x} \right)=m.....\left( ii \right)\]
First, we need to know about the domain of \[{{\sec }^{-1}}x\] i.e. \[\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)\].
Now, try to relate values of \[\dfrac{x}{\sin x}\] and \[\dfrac{x}{\tan x}\] for limit \[x\to 0\], if value inside of \[{{\sec }^{-1}}\left( {} \right)\] will lie in \[\left( -1,1 \right)\] then limit will not exist and if value inside the bracket lies in \[\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)\]. Hence limit will exist.
Let us first relate \[\dfrac{x}{\sin x}\].
One can relate x with sin x and tan x by calculating tangent equations of tan x and sin x at (0, 0) and relate it with y = x.
We know that one can find tangent at any point lying on the curve by calculating slope at that point. Let the point be \[\left( {{x}_{1}},{{y}_{1}} \right)\] and curve is y = f (x) then tangent at \[\left( {{x}_{1}},{{y}_{1}} \right)\] can be given by \[y-{{y}_{1}}={{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\left( x-{{x}_{1}} \right)\]
Tangent equation for sin x at (0, 0) is
\[y-0={{\left. \dfrac{d}{dx}\left( \sin x \right) \right|}_{\left( 0,0 \right)}}\left( x-0 \right)\]
\[y={{\left. \cos x \right|}_{\left( 0,0 \right)}}\left( x \right)\text{ }\left[ \because \dfrac{d}{dx}\sin x=\cos x \right]\]
\[y=x\]
Hence, \[y=x\] is tangent for \[y=\sin x\].
Draw graph of x and sin x in one coordinate plane as follows:

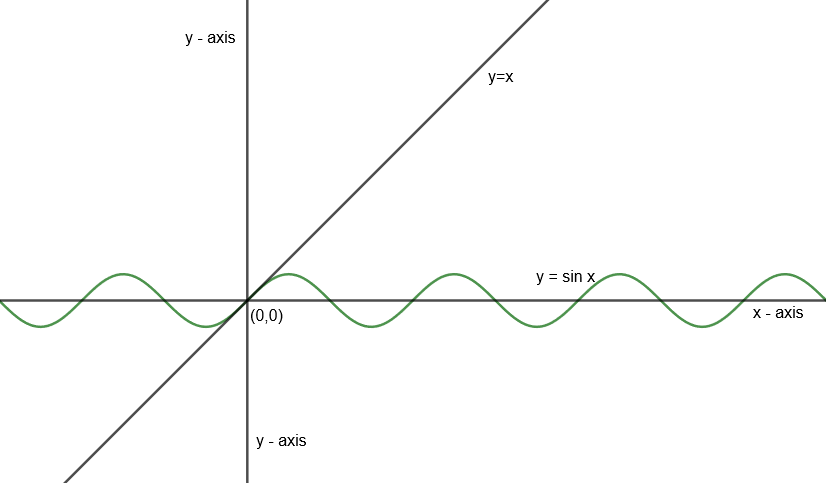
Now for the second case i.e. \[\dfrac{x}{\tan x}\], we get the tangent equation of tan x at (0, 0) is
\[y-0={{\left. \dfrac{dy}{dx} \right|}_{\left( 0,0 \right)}}\left( x-0 \right)\]
\[y={{\left. {{\sec }^{2}}x \right|}_{\left( 0,0 \right)}}\left( x \right)\text{ }\left[ \dfrac{d}{dx}\tan x={{\sec }^{2}}x \right]\]
\[y=x\]
Hence, y = x is tangent for \[y=\tan x\] as well.
Let us draw the graph of x and tan x as follows:

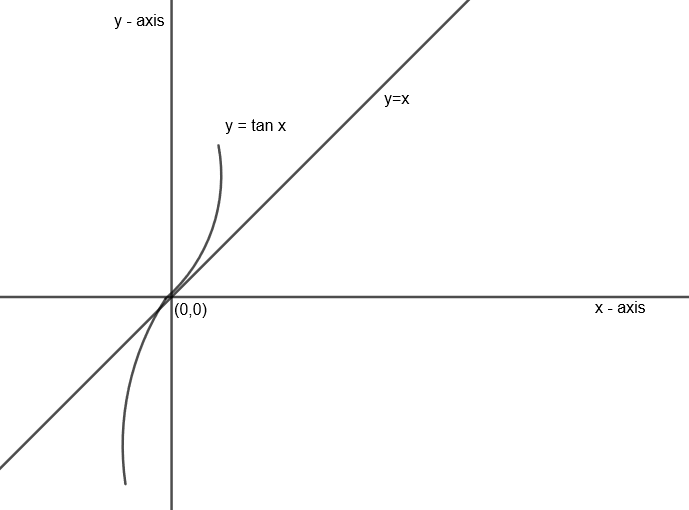Now from the graphs, we can relate for \[\dfrac{x}{\sin x}\] that is:
Case 1: \[x\to {{0}^{+}}\]
We observe x > sin x
Hence, \[\dfrac{x}{\sin x}>1\]
Case 2: \[x\to {{0}^{-}}\]
Here, sin x has a higher positive magnitude than x. Hence, if we put a negative sign to both x and sin x, then
\[x>\sin x\]
\[\dfrac{x}{\sin x}>1\]
Hence, from case 1 and case 2, we get
If \[\lim x\to 0,\] then \[\dfrac{x}{\sin x}>1....\left( iii \right)\]
Similarly, let us relate x and tan x for \[x\to 0\]
Case 1: \[x\to {{0}^{+}}\]
x < tan x
\[\dfrac{x}{\tan x}<1\]
Case 2: \[x\to {{0}^{-}}\]
x < tan x
\[\dfrac{x}{\tan x}<1\]
Hence, for \[x\to 0\], we have \[\dfrac{x}{\tan x}<1....\left( iv \right)\]
Now, for limit ‘l’ from equation (i), we get
\[l=\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)\]
As we have \[\dfrac{x}{\sin x}>1\] from equation (iii) and domain of \[{{\sec }^{-1}}x\] is \[\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)\] as explained in the starting. Hence, we can put \[\lim x\to 0\] to the given relation.
So, \[l=\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)\] will exist.
For limit ‘m’ from equation (ii), we get
\[m=\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\tan x} \right)\]
We have already calculated that \[\dfrac{x}{\tan x}<1\] from equation (iv) and domain of \[{{\sec }^{-1}}x\] is \[\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)\]. Hence the given limit will not exist.
Hence, option (a) is the correct answer to the given problem.

Note: One can directly put \[\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\sin x}=1\] and \[\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\tan x}=1\] as we generally use but that will be wrong for the given expression. As the exact value of \[\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\sin x}\] and \[\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\tan x}\] is not exactly 1, it’s the limiting value of the given expressions. Hence, be careful with these kinds of problems. Relating x with tan x and sin x by calculating tangent at (0, 0) for sin x and tan x is the key point of the question.