Question

Let z1 and z2 be two complex numbers such that z1 $\ne $ z2 and |z1| = |z2|. If z1​ has positive real part and z2​ has negative imaginary part, then $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$ may be which of the following:
(a) Purely imaginary
(b) Real and positive
(c) Real and negative
(d) None of these

Answer 1

Hint: Consider vectors along the position vector of z1​ and z2​ in the Argand Plane and with magnitude equal to |z1| and |z2|. A rhombus will be formed as shown in the figure with z1 + z2 and z1 - z2 in the directions of the diagonals. Use the fact that the diagonals of a rhombus are perpendicular to each other to get z1 + z2 and z1 - z2 will be perpendicular to each other. This means that $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$ will have an argument of $\pm \dfrac{\pi }{2}$ which gives us the final answer.

Complete step by step answer:
In this question, we are given that z1 and z2 are two complex numbers such that z1 $\ne $ z2 and |z1| = |z2|. Also, z1​ has a positive real part and z2​ has a negative imaginary part.
Using this information, we need to find the nature of $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$.
We are given that |z1| = |z2|.
Consider vectors along the position vector of z1​ and z2​ in the Argand Plane and with magnitude equal to |z1| and |z2|.
A rhombus will be formed. Consider the rhombus formed as shown in the figure below:

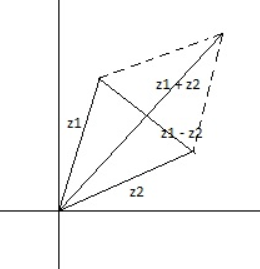
The vector along z1 + z2 ​ will be in the direction of one of the diagonals, while the vector along z1 - z2 ​ will be along the direction of the other diagonal.
We know that the diagonals of a rhombus are perpendicular to each other.
Hence, z1 + z2 and z1 - z2 will be perpendicular to each other
So, $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$ will have an argument of $\pm \dfrac{\pi }{2}$.

Hence, $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$ will be purely imaginary.
So, option (a) is correct.

Note: We can solve this question by another lengthy method also. Let z1 = a + bi and z2 = c + di. Now, find $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$by substituting these. Simplify this and then use the fact that |z1| = |z2| to get ${{a}^{2}}+{{b}^{2}}={{c}^{2}}+{{d}^{2}}$. Substitute this in the previous expression to get the answer.Students should remember if z1 + z2 and z1 - z2 are perpendicular to each then $\dfrac{{{z}_{1}}+{{z}_{2}}}{{{z}_{1}}-{{z}_{2}}}$ will have an argument $\pm \dfrac{\pi }{2}$.
which says the real part is 0 i.e It is purely imaginary.