Question

Light passes through a rectangular glass slab and through a triangular glass prism. In what way does the direction of the two emergent beams differ and why?

Answer 1

Hint: Light travelling from one medium into another tends to change its path or bend a little due to the difference in the refractive indices of the mediums. As given in the question the mediums in the two cases are air, glass, air respectively. So the difference in the two emergent rays must depend upon some other factor, namely the physical structure of the two given quantities.

Complete Step-by-Step solution :
When light travels from one medium to another it tends to bend a little, either towards the normal at the point of incidence or away from the normal at the point of incidence. This bend in the path of the light ray depends upon the refractive index of the two mediums, namely, the one in which the light ray was already travelling and the one it is entering.
⦁When light travels from a denser medium to a rarer medium, it bends away from the normal.
⦁When light travels from a rarer medium to a denser medium, it bends towards the normal.
This bend in the light’s path occurs due to the change in the velocity of the light when travelling between media.
Now, when light enters the glass slab, it emerges from the glass slab in direction parallel to which it entered. In this case the perpendicular distance between incident ray and emergent ray coming out of the glass slab is called lateral displacement.

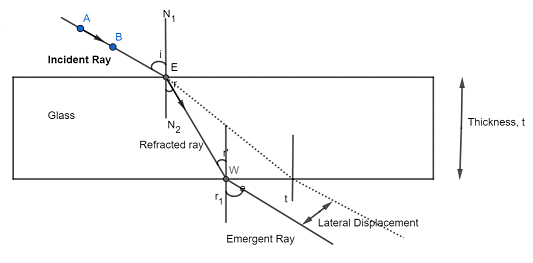
Light ray travelling through a rectangular glass slab
This is a lateral displacement, L of the incident ray through the rectangular glass slab of thickness, t is given by:
$L = t\dfrac{{\sin \left( {i - r} \right)}}{{\cos r}}$
But, when light ray enters through a glass prism, the emergent ray is not parallel to the incident ray after refraction. Rather, the emergent ray deviates from its original direction by a certain angle, known as the angle of deviation.

Light ray travelling through triangular glass prism
$\eqalign{
  & {\text{In case of a prism the deviation, }}{\delta _m}{\text{ of the emergent ray is given by:}} \cr
  & \mu {\text{ = }}\dfrac{{\dfrac{{A + {\delta _m}}}{2}}}{{\sin \dfrac{A}{2}}} \cr
  & {\text{If the angle of prism A is small,}} \cr
  & {\delta _m}{\text{ is also small}}{\text{. So the equation becomes:}} \cr
  & {\delta _m} = \left( {\mu - 1} \right)A \cr} $
⦁Emergent beam of triangular prism is not parallel to its incident beam
⦁In rectangular glass slab emergent ray is parallel to incident ray.
This is because in rectangular glass slab opposite sides are equal and parallel to each other but in triangular prism sides can be equal but not parallel.

Note: Another way to understand this concept of refraction of light when travelling from one medium to another is Snell’s law.
Snell's law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of phase velocities in the two media, or equivalent to the reciprocal of the ratio of the indices of refraction.
Mathematically,
$\dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}} = \dfrac{{{v_2}}}{{{v_1}}} = \dfrac{{{\eta _1}}}{{{\eta _2}}}$

with each $\theta$ as the angle measured from the normal of the boundary, v as the velocity of light in the respective medium and $\eta$ as the refractive index of the respective medium.