Question

What is the limit as x approaches infinity of $\sin \left( x \right)$?

Answer 1

Hint: Assume the required limit as L. Now, to find the value of $\displaystyle \lim_{x \to \infty }\left( \sin x \right)$ first we will draw the graph of the sine function. In the next step we will observe the changes in the graph while we move towards infinity on the x – axis. If the value will be converging to a particular defined number then that will be our answer otherwise we will say that the limit does not exist. We will use the fact $-1\le \sin x\le 1$.

Complete step by step solution:
Here we have been asked to find the limit of the sine function as the domain value, i.e. x, tends to infinity.
Let us assume the limit value as L so mathematically we have,
$\Rightarrow L=\displaystyle \lim_{x \to \infty }\left( \sin x \right)$
As we know that infinity is not a real number so we cannot substitute $x=\infty $ directly in the limit to get its value. Also we don’t know the value of $\sin \left( \infty \right)$. So, we need to use the graphical approach to solve this question. First we will draw the graph of the sine function and check if its value converges to a single point or not as x tends to infinity. So let us draw,

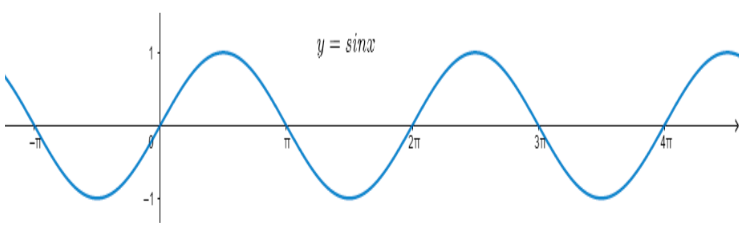
From the above graph we can clearly see that the value of sine function oscillates from -1 to +1. As we keep on increasing the value of x the value of $\sin x$ does not converge to a single point. As infinity is not a certain number so let us say at $x=\infty $ we get any particular value of $\sin x$, but this value will not be fixed because even if we will move a little above or below $x=\infty $ the value of $\sin x$ will increase or decrease, however x will still be infinity.
Hence, we can conclude that the limit does not exist.

Note: Here we do not have any other method to solve the question other than the graphical method because there is no any formula for the simplification of the above limit. You can also find the limits of other trigonometric functions using the similar approach if x is tending to infinity. Remember that the limit of the cosine and the tangent function is also non – existent at $x=\infty $.